Moment-Based Order-Independent Transparency
역자의 말.
언리얼 엔진을 오랫만에 사용하다 보니 아티스트분들이 인터넷에서 봤는지 뭔지 모르겠지만 템포랄 디더 노드를 사용해서 헤어 알파? 처리를 하고 있더라고요. TAA 나 TSR 을 좀 아시는 분들 이라면 템포랄 디더가 어떻게 동작하는지 아시겠지만 Previous frame flag 를 사용하고 있죠.
이 전 프레임과 지금 프레임을 사용해서 AA 효과를 달성? 하고 있는 모양세 입니다.당연히 이대로는 모바일 빌드를 하면 템포랄 디더 노드가 모바일 API 에서 Previous frame flag 를 취할 수 없음으로 점망이 그대로 드러나 보이죠. 물론 전형적인 방법의 멀티페스를 언리얼에서도 구현해서 사용할 수 있기 때문에 알파테스트와 알파브렌드 조합의 2번 그리기를 사용하면 모바일에서 헤어 소팅 문제는 적당히 해결? 할 수 있습니다. 해결이라고 말 하기에는 정확하게는 무리가 있습니다만 말이죠.
유니티에서는 머티리얼 두개를 사용하거나 유니티 API 를 사용해 간단하게 멀티페스를 적용할 수 있습니다( GPU 상주 드로어에서는 그렇게 하면 안됩니다. 정확히 멀티페스를 사용해야 해요) ... 언리얼 에서는 멀티페스를 직접 추가 해 줘야 합니다. 어렵진 않지만 아티스트에게는 좀 먼 이야기일수 있어요(중국개발자의 멀티페스 플러그인도 있어요).
그나저나 오래 전 부터 헤어 정렬에 대해서 깊게 관심이 있었기 때문에 이런 방안도 있다라는 개념으로 기사를 추가 해 봤습니다.
2020년 넷이즈 어떤 스튜디오에서는 SIMD 단에서 최적화 된 CPU 기반 정렬을 사용한다는 케이스에 대해서 들었던 것도 있구요. 물론 매우 고도화 된 프로그래밍 레벨이 요구 되는 것으로 알고 있어서 패싱 했고요... ㅎㅎ
모멘트 기반 순서 독립적 트렌스페런트에 대한 글을 그 당시에 읽었기 때문에 컨설팅을 하고 있는 A 사의 엔지니어들과 이 부분에 대해서 빌드업을 해 보려는 차원에서 개인 저장소에 있던 것을 공유 해 봅니다. 물론 뭐 제가 쓴건 아니구요.. .ㅎㅎ
전언
이전 글 스크린 스페이스 딥 섀도우 맵(스크린 스페이스 딥 섀도우 맵)에 실수가 있었는데, 사실 스크린 스페이스 딥 섀도우 맵을 반투명 오브젝트에 직접 사용할 수 있습니다.
블렌딩 공식에 따르면 화면의 픽셀 포인트에 대해 다음과 같이 계산합니다.
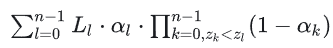
콘텍트 그림자도 화면 공간에 있으므로 화면의 픽셀 포인트에 대한 상수 값이며 공식에서 전적으로 추출할 수 있으므로 얼마나 많은 레이어를 블렌딩하는지는 중요하지 않습니다. (파티클) 연기의 경우, 정렬 후 원거리 및 근거리 방식으로 렌더링한 후 그림자가 채색에 참여하도록 프래그에서 직접 SSDSM의 Lut을 샘플링할 수 있습니다.
하지만 머리카락, 일반적으로 복잡한 기하학적 모델(예: 작은 컬)로 작업하는 경우 모델 자체가 닫혀 있지 않고 자체 교차할 수도 있기 때문에 (슬라이스 수준에서 정렬하지 않는 한) 소팅을 사용하여 반투명 셰이딩 문제를 해결할 수 없는 상황이 발생하기 때문에 이 문제를 해결하기 위해 이 글에서는 모멘트 기반 순서 독립적 투명도 렌더링을 사용합니다.
또한 이 글에서는 스크린 스페이스 딥 섀도맵을 통합하는 방법도 설명합니다.
문제
먼저 다음 질문을 살펴보겠습니다.

기본적인 방법을 사용하여 반투명을 직접 렌더링하면 매우 명백한 오류가 발생합니다.
이것이 왜 문제인가요? 위와 같은 공식입니다:
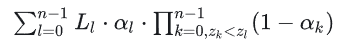
이 공식을 관찰하면 반투명 렌더링을 수행할 때 동일한 화면 좌표에서 어떤 슬라이스가 현재 슬라이스보다 깊이 값이 작은지 알 수 없다는 것을 알 수 있습니다.따라서 정렬이 없는 경우 알파 블렌딩에 기본 블렌드를 직접 사용하면 결과가 잘못됩니다.
그렇다면 이 문제를 어떻게 해결할 수 있을까요?
사실, 딥 섀도우 맵 접근 방식을 참조하여 체인 목록을 사용하여 슬라이스 요소를 정렬할 수 있습니다.이것은 저에게는 그리 어렵지 않고 DX 샘플(참고 11)에 기성 코드가 있으므로 새로운 것을 시도해 볼 수 있으므로 모멘트 기반 순서 독립 투명도(참고 1)를 사용해 보겠습니다.
모멘트 기반 순서 독립적 반투명 렌더링
모멘트 추정은 실제로 분산 섀도 매핑(참고 13)에서도 사용되지만, VSM은 섀도맵의 사전 필터링을 위해 2차 모멘트(기대 및 분산)만 사용하고 섀도맵의 텍스처 공간에서 계산합니다. 모멘트 섀도 매핑(참고 2)은 4차 모멘트에 이어 6차 모멘트로 확장되었고, 반투명 오브젝트의 그림자를 계산하기 위해 (조명 공간의) z축에서 모멘트 추정을 수행했습니다(참고 3).모멘트 기반 순서 독립 투명도는 다시 8차 모멘트로 확장되어 OIT에 적용되었습니다.
확률적 측면을 포함하는 모멘트와 일반화된 모멘트 추정에 대해서는 관심 있는 학생은 참고자료 8과 9를 참조하시기 바라며, 여기서는 자세히 설명하지 않습니다(사실 아직 완전히 이해되지 않았기 때문입니다).
이 논문에서 모멘트는 간단히 말해 현재 슬라이스 요소(카메라의 Z축 방향)가 다른 슬라이스 요소에 의해 가려질 확률을 계산하는 데 사용되며, 이 확률과 전체 투과율(1- 전체 α)을 사용하여 현재 슬라이스 요소가 얼마나 많은 비율의 빛을 수신할 수 있는지 추정하는 데 사용됩니다.
그 효과를 살펴보겠습니다:

불투명 오브젝트 렌더링
먼저 불투명한 물체를 일반적인 순서대로 그려 보겠습니다.
모멘트를 사용하여 흡수율 표현하기
수식 도출의 앞부분은 건너뛰고 계산해야 할 내용을 먼저 살펴보겠습니다:
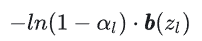
각 슬라이스 요소에 대해 위 공식의 값을 계산한 다음 블렌드 원 원을 사용하여 렌더 타깃에 누적시켜야 합니다:
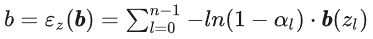
그렇다면 b는 무엇일까요?b는 실제로 벡터입니다:
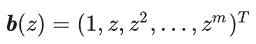
이것은 현재 슬라이스 요소의 깊이가 z인 m+1 차원 모멘트입니다.임펄스 함수 δ의 분포를 반영하며, 다음과 같이 정의됩니다:
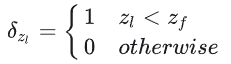
그렇다면 이 펄스 함수 δ는 어떤 역할을 할까요?
첫 번째 방정식으로 돌아가서, 어떤 깊이에서의 빛 감쇠 값을 나타내는 투과율 T를 추출합니다:
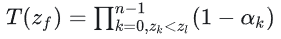
그런 다음 로그 함수를 사용하여 누적 곱셈을 누적 덧셈으로 변환하고 흡수율 함수를 정의합니다:
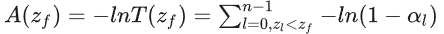
임펄스 함수 δ의 이전 정의에 따라 흡수율 함수 A는 유한 추정 누적 분포 함수로 간주할 수 있습니다.
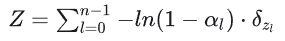
이 함수를 직접 저장할 수 없으므로 앞서 언급한 대로 모멘트를 통해 저장하고 다음 단계에서 근사값을 구성합니다.
투과율 재구성
흡수율에 대한 대략적인 함수 A를 구했다고 가정하면 이 함수를 통해 투과율을 재구성할 수 있습니다:
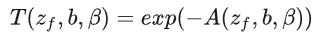
여기서 β는 과대 추정치이며 원본 문서에서는 0.25 값을 제안합니다. 그런 다음 다음 공식에 따라 반투명 오브젝트를 다시 렌더링하고 오프 스크린 렌더 타겟에 저장합니다.
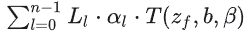
즉, 반투명 오브젝트를 다시 렌더링하고 각 슬라이스에 대해 색상(Ll)에 불투명도 및 투과율을 곱한 다음 블렌드 원 원을 사용하여 합산합니다.그렇다면 알파 채널 내부에는 무엇이 저장될까요?
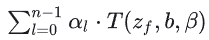
병합 단계에서 쉽게 계산할 수 있도록 알파 채널에 저장됩니다.
Warping Depth(적합한 번역을 찾을 수 없습니다.)
이 부분은 z의 정확도를 개선하고 깊이 값을 다시 계산하는 간단한 작업입니다.
통합
이 단계에서는 반투명 렌더 타깃을 블릿이라고도 하는 불투명 렌더 타깃과 병합합니다. 앞서 모멘트에서 언급했듯이 0번째 모멘트는 픽셀 좌표에서 전체 흡수율을 유지합니다:
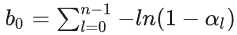
따라서 exp(-b0)는 현재 화면 좌표의 전체 투과율이며, 이 단계를 용이하게 하기 위해 렌더 타깃 내부에 별도로 저장됩니다.
그런 다음 이 단계에서 이를 기반으로 병합할 수 있습니다:
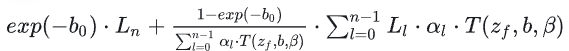
분모의 일부는 에너지 보존을 근사화하기 위한 정규화에 사용되며, 이 값은 투과율을 재구성하는 단계에서 반투명 렌더 타깃의 알파 채널에 저장되어 있으므로 RGB 채널의 값으로 직접 나눈 다음 Blend OneMinusSrcAlpha SrcAlpha (알파 채널은 exp(-b0) 사용) 방식으로 사용됩니다.불투명 렌더 타깃에 블릿합니다.
무력한 순간 (수학)
이 모든 것을 말했지만, 가장 중요한 부분 중 하나, 즉 흡수율의 대략적인 함수 A를 구하는 방법이 앞서 건너뛰었다는 것을 눈치 채셨을 것입니다.
앞서 b는 m+1 차원 모멘트라고 언급했습니다:
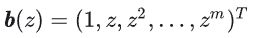
원글에서는 4차, 6차, 8차 힘모멘트와 2차, 3차, 4차 삼각모멘트를 사용하는데, 삼각모멘트의 효과는 조금 뜨거워서 이 글에서는 생략하고 힘모멘트를 사용하여 푸는 방법만 간략하게 설명합니다.또한 4차, 6차, 8차는 해법에서 거의 차이가 없으므로(8차는 4차 다항식을 풀어야 하므로 앞의 두 가지보다 더 복잡함) 이 글에서는 4차 힘모멘트 해법을 예로 들어 설명합니다. (여기서는 단계만 설명하며, 구체적인 증명은 참고자료 17에 있습니다.)
콜레스키 분해
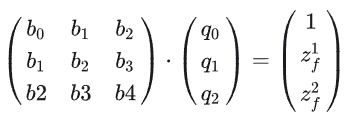
먼저 위 방정식에서 q 벡터(zf는 현재 슬라이스 요소의 워핑 깊이)를 풀어야 하는데, 여기서 콜레스키 분해가 사용됩니다.
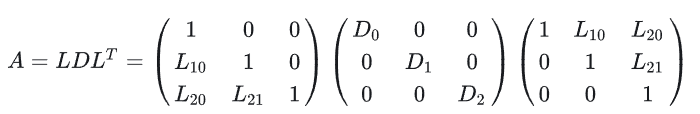
분해 후에는 풀이 난이도가 극적으로 단순화됩니다.
임펄스 분포 함수 구축하기
그런 다음 다항식을 풉니다:
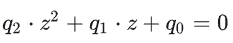
z1 및 z2를 얻고 펄스 분포 함수를 구성합니다. zl이 zf보다 작으면 vl은 1이고, 그렇지 않으면 0입니다.
Vandermonde행렬
다음으로 방데르몽 행렬을 풉니다.
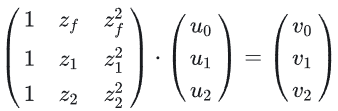
여기서 v0은 과대 추정이고 원본 논문에서는 0.25의 값을 제안합니다. 가중치 값 u0, u1 및 u2를 얻습니다.
재건 흡수율
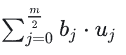
흡수율 A는 위의 방정식에 의해 재구성되며 투과율은 exp(-A)와 같습니다.
퓨전 섀도
글 서두의 결론에 따르면 이 단계는 원칙적으로는 위의 투과율을 재구성하는 단계에서 셰이딩(조명) 계산에 그림자 값을 추가하면 되므로 간단하지만 실제로는 스크린 스페이스 딥 섀도맵에는 카메라 깊이 맵과 반투명 오브젝트의 깊이가 필요하고 반투명 오브젝트의 깊이가 불투명 오브젝트의 깊이를 오염시키지 않으려면 별도의 렌더 대상이 필요하므로 약간 까다로운 작업이라고 합니다.반투명 오브젝트의 깊이가 불투명 오브젝트의 깊이를 오염시키는 것을 원하지 않으므로 별도의 렌더 타겟이 필요합니다. 깊이 사전 렌더링 후 깊이 텍스처를 OIT 깊이 텍스처로 복사한 다음 반투명 오브젝트의 깊이를 그 위에 그립니다.그리고 스크린 스페이스 딥 섀도맵 정착 단계를 변경하여 이 RT를 샘플링합니다.
효과는 그림과 같습니다:

전체 구현은 제 깃허브에 올렸습니다:
https://github.com/ecidevilin/KhaosLWRP
GitHub - ecidevilin/KhaosLWRP
Contribute to ecidevilin/KhaosLWRP development by creating an account on GitHub.
github.com
참고 문헌
- 1.Moment-Based Order-Independent Transparency
- 2. Moment Shadow Mapping
- 3. Improved Moment Shadow Maps for Translucent Occluders, Soft Shadows and Single Scattering
- 4. Moment-Based Methods for Real-Time Shadows and Fast Transient Imaging
- 5. Solving trigonometric moment problems for fast transient imaging
- 6. Non-linearly Quantized Moment Shadow Maps
- 7. Introduction to Probability
- 8. 概率论中「矩」(moment)的实际含义是什么,高阶矩表示数据的哪些状态? - 荆哲的回答 - 知乎
- 9. 如何用简单的例子解释什么是 Generalized Method of Moments (GMM)? - 慧航的回答 - 知乎
- 10. Web端的实时透明渲染算法
- 11. DirectX Software Development Kit
- 12. ShaderX6
- 13. Variance Shadow Mapping (http://www.punkuser.net/vsm/)
- 14. Variance Shadow Mapping (NVidia) (https://developer.download.nvidia.com/SDK/10/direct3d/Source/VarianceShadowMapping/Doc/VarianceShadowMapping.pdf)
- 15. Exponential Shadow Maps (http://jankautz.com/publications/esm_gi08.pdf)
- 16. Advanced Soft Shadow Mapping Techniques (https://developer.download.nvidia.com/presentations/2008/GDC/GDC08_SoftShadowMapping.pdf)
- 17. Supplementary Document on Moment Shadow Mapping