저자
시바마마 부추꽃(인터넷명)

一.원칙 소개
1.아이디어 분석
매체의 시뮬레이션을 바라보는 두 가지 관점, 즉 라그랑주 관점과 오일러 관점부터 살펴보겠습니다.

라그랑주 관점은 일반적으로 매질을 매질과 함께 움직이는 입자(또는 작은 격자)의 집합으로 보고 각 입자의 운동 상태와 힘을 계산하여 매질의 변화를 표현합니다. 반면 오일러 관점은 일반적으로 매체가 차지하는 공간을 작은 격자로 나누고 각 작은 격자에 대해 격자 내의 매체의 상태, 입력 및 출력, 나머지 격자에 미치는 영향을 계산합니다.
특정 지점의 풍력을 계산하려면 라그랑지안 원근법을 사용하면 해당 지점을 통과하는 단위 시간당 평균 입자 속도를 구해야 하는데, 단위 시간당 입자가 지점을 통과할 확률이 낮기 때문에 현실적이지 않은 것이 분명합니다. 오일러 원근법을 사용하면 포인트가 위치한 그리드 위치만 찾으면 되므로 평균 속도를 직접 읽을 수 있습니다.
GDC 2019에서 갓 오브 워의 풍력 발전소 기술 공유도 오일러 관점의 실현을 기반으로 했습니다.

배틀스타 갤럭티카 인터랙티브 풍력 발전소 공유

로컬 속도 필드
플레이어의 동작은 속도 필드의 변화에 영향을 줄 수 있으며, 이는 다시 씬의 오브젝트에 힘을 가할 수 있습니다.
배틀스타 갤럭티카의 접근 방식은 32x32x16미터 영역을 그리드당 1미터의 정확도로 나누어 그리드 내의 평균 속도를 기록하고, 전체 속도 필드는 캐릭터의 움직임을 따라가며 씬 상호작용에 대한 효과는 해당 영역 내에서만 발생하도록 하는 것입니다. 그 이상은 노이즈로 샘플링되거나 기본 속도가 지정되어 그리드가 전체 월드 공간에 퍼지지 않도록 하여 비용을 절약할 수 있습니다.
이제 전체 바람 필드가 필드를 기반으로 한다는 것을 알았으니 플레이어가 필드를 어떻게 변화시키고, 필드는 현실에서 물리 법칙에 따라 어떻게 변화를 겪을까요? 이에 대한 고전적인 논문인 '게임용 실시간 유체 역학'을 살펴보겠습니다.
知乎 - 安全中心
即将离开知乎 您即将离开知乎,请注意您的帐号和财产安全。 http://graphics.cs.cmu.edu/nsp/course/15-464/Fall09/papers/StamFluidforGames.pdf
link.zhihu.com
2.분석 에세이
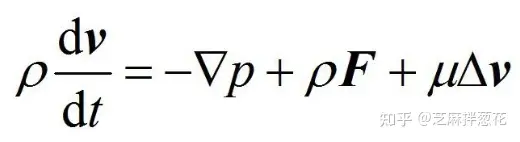
나비에-스토크스 방정식
안정 유체는 나비에-스토크스 방정식 체계를 기반으로 하며 유체 시뮬레이션으로 선호됩니다. 여기서 유체는 비압축성(비점성) 유체이므로 밀도와 온도가 일정합니다. 여기서 P는 압력장(스칼라 필드), p는 밀도, v는 점도 계수(점성), F는 외력을 나타냅니다.

일반 방정식 (1)의 N-S는 다음과 같이 변형될 수 있습니다.

첫 번째 항인 F는 잘 알려져 있으며 외력을 나타냅니다. 이는 속도 필드에 추가되는 외력을 나타내는 논문의 AddSource 항에 해당하며, 게임에서 유체 상호작용은 주로 외력의 적용에 반영됩니다.
논문에서 두 번째 항인 확산 항은 액체의 점성으로 간단히 이해할 수 있으며, 이 항은 속도가 자체 2차 도함수에 따라 확산되고 있음을 나타냅니다. 확산이 강할수록 필드가 더 부드러워집니다. 오일러 관점은 각 셀과 주변 이웃 사이의 교환으로 표현됩니다. 이상적으로 교환은 다음과 같이 표현할 수 있습니다:

세포액 간 이상적인 교환
x = x0 +a*(sum_p – num* x0 )*dt
여기서 x0은 이전 상태, x는 현재 상태, a는 확산 속도, num은 이웃 셀의 수, sum_p와 sum_c는 각각 이전 순간과 다음 순간의 이웃 셀 값의 합입니다.
이 논문의 저자는 두 번째 항을 직접 풀면 음수가 될 수 있고 흔들림과 발산을 일으킬 수 있다고 판단하여 그렇게 하지 않았습니다. 따라서 그는 방정식을 다음과 같이 변형했습니다:
x0 = x - a*(sum_c – num*x)*dt
x0= x – a*sum_c*dt+a*num*x*dt
(1+a*num*dt)x = x0+a*sum_c*dt
x = (x0+a*sum_c*dt)/(1+a*num*dt)
이 논문은 이 해에 역수가 필요하지 않다고 주장하며, 대신 저자들은 방정식 시스템을 여러 번 반복하여 점차적으로 근사치를 구하는 Gauss-Seidel Relaxation 방법을 사용합니다.。
세 번째 항은 논문에서 속도가 자체 방향으로 움직이는 대류 항(어드벡트)에 해당합니다. 유체의 속도는 유체가 흐름과 함께 물체, 밀도 및 기타 양을 운반하게 만든다는 것을 이해할 수 있습니다. <여기서 유체는 속도에 따라 움직이는 개별 입자로 생각할 수 있으며, 저자들은 논문에서 세미 라그랑지안 접근법을 사용합니다:

(수학.) 세미 라그랑지안 방법
각 셀의 중심을 입자로 간주하고 속도 필드를 따라 역추적하여 dt 순간 이전 어느 위치에 있던 입자가 현재 위치로 이동할지(s=so+v*dt, so=s-v*dt), dt 시간 입자를 선형 보간하고 이 입자를 현재 시점의 입자로 간주합니다.
<네 번째 항은 논문에서 투영 항에 해당하며, 압력 p를 푸는 데 중점을 둡니다. 유체의 분자는 서로 움직일 수 있기 때문에 "찌그러지거나" "흔들리는" 경향이 있습니다. 유체에 힘이 가해지면 그 힘은 즉시 부피 전체에 전파되지 않습니다. 대신 힘에 가까운 분자가 더 멀리 있는 분자를 밀어내면서 압력이 증가합니다. 압력은 단위 면적당 힘이기 때문에 유체의 모든 압력은 자연스럽게 가속으로 이어집니다. 저자들은 논문에서 p를 세 단계로 나누어 풀었습니다:
첫 번째 단계에서 산란장은 푸아송 방정식을 푸는 의미에서 음수, 즉 -1을 곱하는 연산이 하나 줄어든 음수임을 알 수 있습니다.
-div = -0.5*(ui+1 – ui-1+ vi+1 – vi-1 + wi+1 – wi-1)/dx두 번째 단계에서는 헬름홀츠-호지 분해 정리가 사용됩니다, 즉 모든 벡터 필드는 분산 벡터 필드와 그라데이션 스칼라 필드로 분해할 수 있습니다. 즉, 이 산란 필드의 원인이 되는 필드 p의 2차 도함수가 무엇인지 알아내는 것입니다. 여기서는 앞서 확산 항을 풀 때 사용한 것과 유사한 반복 방법을 사용하여 이를 수행합니다.
亥姆霍兹分解
(建议 阅读最新版本) 预备知识 散度的逆运算,旋度的逆运算 1任何矢量场都可以分解为一个无旋场 \boldsymbol{\mathbf{F}} _{d}( \boldsymbol{\mathbf{r}} ),一个无散场 \boldsymbol{\mathbf{F}} _{c}( \boldsym…
zhuanlan.zhihu.com
세 번째 단계에서는 p를 풀고, p의 그라데이션 필드를 뺍니다로, 속도를 구하면 소위 투영을 만족하여 안정성을 보장합니다.
u -=(p[i+1,,]-p[i-1,,])/2dx
v -=(p[,j+1,]-p[,j-1,])/2dx二.구현 프로세스
UE에서 GPU 유체 시뮬레이션을 구현하는 방법은 여러 가지가 있는데, 더 유명한 피우드닌자 유체 플러그인은 다이내믹 머티리얼 인스턴스에서 RT로 출력을 계산하여 구현하는 등 이 문서에서는 나이아가라에서 GPU 시뮬레이션 단계의 프로세스 구현에 중점을 두고 있습니다.
1.인프라

빈 이미터를 생성하고 심 타깃을 GPUCompute Sim으로 변경한 다음 고정 바운드를 생성합니다;

사용자 노출에서
출력 디버깅을 위한 RT로 WindFieldRT라는 이름의 Texture Render Target 유형 변수를 생성합니다.
렌더링 대상에 대한 해상도로 해상도라는 이름의 int 유형 변수를 생성합니다.


이미터 속성에서
Grid3D 컬렉션 유형에 VelocityGrid라는 이름의 변수를 만들고, Num Attribute를 3으로 설정합니다.
Render Target 2D 유형의 변수를 RT_WindField라는 이름으로 만들고, 오버 렌더 타깃 포맷을 RGBA 16f로 설정하고, 렌더 타깃 사용자 파라미터를 방금 만든 WindFieldRT로 설정합니다. WindFieldRT로 설정합니다.
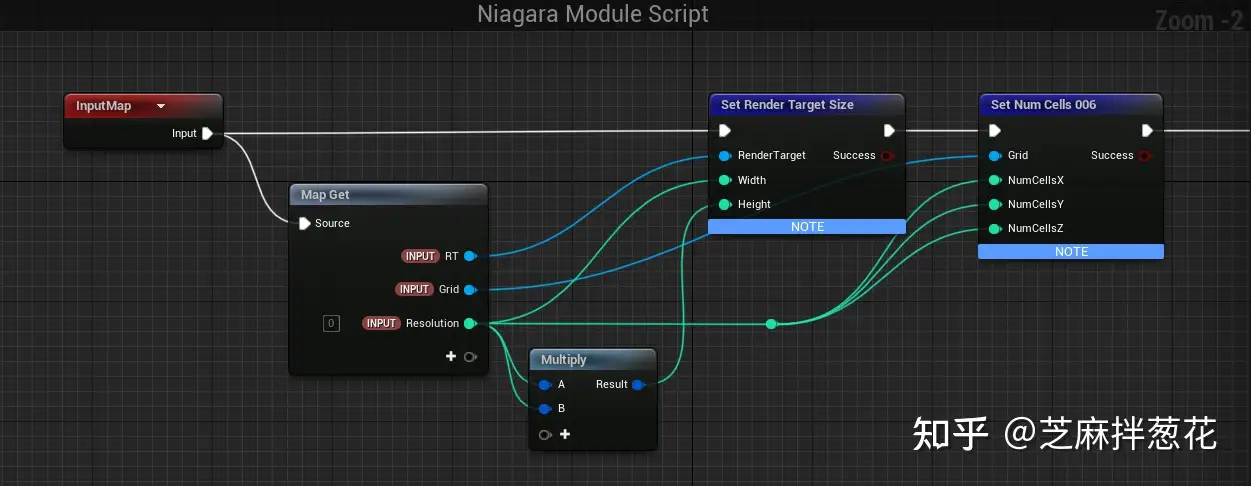
NMS_SetResolution이라는 이름의 나이아가라 무들 스크립트를 생성하여 VelocityGrid 그리드 번호와 RT_WindField 해상도를 설정합니다. 여기서 3D 그리드를 2D RT에 쓰고, Z축 슬라이싱과 Y축 타일링을 사용해야 한다는 점에 유의하세요. 따라서 렌더링 대상 해상도는 (x,y*z)입니다.

NMS_ExportToRT라는 이름의 나이아가라 무들 스크립트를 생성하여 Grid3D에서 RT로 정보를 씁니다. 이때 Grid3D의 값을 변경해 볼 수 있으며, RT도 함께 변경되면 Grid3D에서 RT로 쓰기가 성공했음을 증명합니다.
다음 계산은 각각 별도의 시뮬레이션 스테이지에서 수행해야 하며, 동일한 스테이지 아래에 배치하면 동시 병렬 계산으로 간주될 수 있으므로 입력 그리드는 이전 프레임의 계산 결과입니다.

RT_WindField라는 이름의 렌더 타깃 시트를 만듭니다.
액터 블루프린트를 생성하고 나이아가라 컴포넌트를 추가한 다음 WindFieldRT 파라미터를 방금 생성한 RT_WindField로 설정하고 해상도를 128로 설정합니다.
블루프린트를 씬으로 드래그합니다.
2.AddSource(외력 항)
여기서 외부 힘은 유체에 대한 외부 영향의 주요 원인인 충돌에 의해 생성되는 힘으로만 간주됩니다. 특정 위치가 캐릭터와 충돌하는지 여부를 확인하려면 먼저 Grid3D의 인덱싱된 위치에서 월드 위치로 축소해야 합니다.

여기서 입력 항목 Grid는 속도 그리드, Size는 사용자 지정 풍력 발전 단지 시뮬레이션 범위, WorldPosition은 풍력 발전 단지 구성 요소가 위치한 세계 위치입니다. 각 셀이 위치한 세계 위치가 계산됩니다.
cellWorldPosition = (float3(x,y,z) / res) * size + worldPosition;
콜리전 감지 소스에 피직스 에셋>을, 단위 시간에 dt>를 새 입력으로 추가합니다. 여기서는 엔진 제공의 델타타임>을 사용합니다.
가장 가까운 요소 가져오기 노드에 셀 월드 포지션 을 입력하여 가장 가까운 위치 점의 가장 가까운 거리(Closest Distance)와 속도(Closest Velocity)를 구합니다. . 여기서 판단해야 할 사항이 있는데, 위치 포인트가 피직스 에셋 내부에 있을 때 Closest Distance 값은 음수이고 피직스 에셋과 교차하는 부분의 위치 포인트의 속도만 필요하며 다른 위치 속도는 의미가 없습니다. 이 속도를 최종적으로 이전 프레임의 속도와 겹쳐진 속도 소스로 사용합니다.

3.Diffuse(확산 용어(수학))

float a = dt * diff * N * N * N;
float VX_self;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex, VX_self);
float VX_right;
Grid.GetGridValue(IndexX+1, IndexY, IndexZ, VectorIndex, VX_right);
float VX_left;
Grid.GetGridValue(IndexX-1, IndexY, IndexZ, VectorIndex, VX_left);
float VX_up;
Grid.GetGridValue(IndexX, IndexY+1, IndexZ, VectorIndex, VX_up);
float VX_down;
Grid.GetGridValue(IndexX, IndexY-1, IndexZ, VectorIndex, VX_down);
float VX_front;
Grid.GetGridValue(IndexX, IndexY, IndexZ+1, VectorIndex, VX_front);
float VX_back;
Grid.GetGridValue(IndexX, IndexY, IndexZ-1, VectorIndex, VX_back);
float VY_self;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex + 1, VY_self);
float VY_right;
Grid.GetGridValue(IndexX+1, IndexY, IndexZ, VectorIndex + 1, VY_right);
float VY_left;
Grid.GetGridValue(IndexX-1, IndexY, IndexZ, VectorIndex + 1, VY_left);
float VY_up;
Grid.GetGridValue(IndexX, IndexY+1, IndexZ, VectorIndex + 1, VY_up);
float VY_down;
Grid.GetGridValue(IndexX, IndexY-1, IndexZ, VectorIndex + 1, VY_down);
float VY_front;
Grid.GetGridValue(IndexX, IndexY, IndexZ+1, VectorIndex + 1, VY_front);
float VY_back;
Grid.GetGridValue(IndexX, IndexY, IndexZ-1, VectorIndex + 1, VY_back);
float VZ_self;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex + 2, VZ_self);
float VZ_right;
Grid.GetGridValue(IndexX+1, IndexY, IndexZ, VectorIndex + 2, VZ_right);
float VZ_left;
Grid.GetGridValue(IndexX-1, IndexY, IndexZ, VectorIndex + 2, VZ_left);
float VZ_up;
Grid.GetGridValue(IndexX, IndexY+1, IndexZ, VectorIndex + 2, VZ_up);
float VZ_down;
Grid.GetGridValue(IndexX, IndexY-1, IndexZ, VectorIndex + 2, VZ_down);
float VZ_front;
Grid.GetGridValue(IndexX, IndexY, IndexZ+1, VectorIndex + 2, VZ_front);
float VZ_back;
Grid.GetGridValue(IndexX, IndexY, IndexZ-1, VectorIndex + 2, VZ_back);
float3 V_self = float3(VX_self,VY_self,VZ_self);
float3 V_right = float3(VX_right,VY_right,VZ_right);
float3 V_left = float3(VX_left,VY_left,VZ_left);
float3 V_up = float3(VX_up,VY_up,VZ_up);
float3 V_down = float3(VX_down,VY_down,VZ_down);
float3 V_front = float3(VX_front,VY_front,VZ_front);
float3 V_back = float3(VX_back,VY_back,VZ_back);
diffusion = (V_self + a * (V_right + V_left + V_up + V_down + V_front + V_back)) / (1 + 6 * a);위에서 도출된 x = (x0+a*sum_c*dt)/(1+a*num*dt)의 반복(10회 이상 반복 횟수)에 대한 샘플은 확산 계수에 대한 입력 diff를 외부에서 입력할 수 있으며, 값이 클수록 셀 간의 교환 속도가 빨라지고 유체의 성능 효과가 더 희석되며 반대가 진해질수록 그 효과가 커집니다.
4.Advect(전진 용어 (수학))

float dt0 = dt * N;
float i = IndexX;
float j = IndexY;
float k = IndexZ;
float U;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex, U);
float V;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex + 1, V);
float W;
Grid.GetGridValue(IndexX, IndexY, IndexZ, VectorIndex + 2, W);
float x = i - dt0 * U;
float y = j - dt0 * V;
float z = k - dt0 * W;
x = clamp( x, 0.5, N + 0.5);
y = clamp( y, 0.5, N + 0.5);
z = clamp( z, 0.5, N + 0.5);
int x0 = int(x);
int y0 = int(y);
int z0 = int(z);
float x1 = x0 + 1;
float y1 = y0 + 1;
float z1 = z0 + 1;
float xd = (x - x0) / (x1 - x0);
float yd = (y - y0) / (y1 - y0);
float zd = (z - z0) / (z1 - z0);
float VX000;
Grid.GetGridValue(x0, y0, z0, VectorIndex, VX000);
float VX100;
Grid.GetGridValue(x1, y0, z0, VectorIndex, VX100);
float VX010;
Grid.GetGridValue(x0, y1, z0, VectorIndex, VX010);
float VX001;
Grid.GetGridValue(x0, y0, z1, VectorIndex, VX001);
float VX101;
Grid.GetGridValue(x1, y0, z1, VectorIndex, VX101);
float VX011;
Grid.GetGridValue(x0, y1, z1, VectorIndex, VX011);
float VX110;
Grid.GetGridValue(x1, y1, z0, VectorIndex, VX110);
float VX111;
Grid.GetGridValue(x1, y1, z1, VectorIndex, VX111);
float VY000;
Grid.GetGridValue(x0, y0, z0, VectorIndex + 1, VY000);
float VY100;
Grid.GetGridValue(x1, y0, z0, VectorIndex + 1, VY100);
float VY010;
Grid.GetGridValue(x0, y1, z0, VectorIndex + 1, VY010);
float VY001;
Grid.GetGridValue(x0, y0, z1, VectorIndex + 1, VY001);
float VY101;
Grid.GetGridValue(x1, y0, z1, VectorIndex + 1, VY101);
float VY011;
Grid.GetGridValue(x0, y1, z1, VectorIndex + 1, VY011);
float VY110;
Grid.GetGridValue(x1, y1, z0, VectorIndex + 1, VY110);
float VY111;
Grid.GetGridValue(x1, y1, z1, VectorIndex + 1, VY111);
float VZ000;
Grid.GetGridValue(x0, y0, z0, VectorIndex + 2, VZ000);
float VZ100;
Grid.GetGridValue(x1, y0, z0, VectorIndex + 2, VZ100);
float VZ010;
Grid.GetGridValue(x0, y1, z0, VectorIndex + 2, VZ010);
float VZ001;
Grid.GetGridValue(x0, y0, z1, VectorIndex + 2, VZ001);
float VZ101;
Grid.GetGridValue(x1, y0, z1, VectorIndex + 2, VZ101);
float VZ011;
Grid.GetGridValue(x0, y1, z1, VectorIndex + 2, VZ011);
float VZ110;
Grid.GetGridValue(x1, y1, z0, VectorIndex + 2, VZ110);
float VZ111;
Grid.GetGridValue(x1, y1, z1, VectorIndex + 2, VZ111);
float3 V000 = float3(VX000,VY000,VZ000);
float3 V100 = float3(VX100,VY100,VZ100);
float3 V010 = float3(VX010,VY010,VZ010);
float3 V001 = float3(VX001,VY001,VZ001);
float3 V101 = float3(VX101,VY101,VZ101);
float3 V011 = float3(VX011,VY011,VZ011);
float3 V110 = float3(VX110,VY110,VZ110);
float3 V111 = float3(VX111,VY111,VZ111);
//三线性差值
Advect = V000 * (1 - xd) * (1 - yd) * (1 - zd) +
V100 * xd * (1 - yd) * (1 - zd) +
V010 * (1 - xd) * yd * (1 - zd) +
V001 * (1 - xd) * (1 - yd) * zd +
V101 * xd * (1 - yd) * zd +
V011 * (1 - xd) * yd * zd +
V110 * xd * yd * (1 - zd) +
V111 * xd * yd * zd;
그림과 같이 (각 작은 셀의 측면 길이는 0.25) 현재 프레임(노란색 점 위치)에서 셀의 속도는 (2.75,1.25)이고, 이전 프레임의 위치(파란색 점)로 역 추적하여 그 점에 인접한 셀의 값을 선형 차이로 표본화하여 결과를 다음 프레임의 속력으로 얻는 이 단계는 주로 세미 라그랑지안 방법을 구현하는 것입니다([1] 참조). .
5.Project(투영 기간)

분산 및 압력 구배를 계산하기 위해 DivergenceGrid와 PressureGrid라는 두 개의 Grid2D가 생성됩니다. 여기서는 현재 속도 필드의 산란 필드, 헬름홀츠 분해 정리에 따른 반복을 통해 속도 필드의 구배 필드, 구배 필드의 차감을 통해 속도 필드를 계산하는 세 가지 시뮬레이션 단계로 나눴습니다.

분산 계산

구배 압력 계산
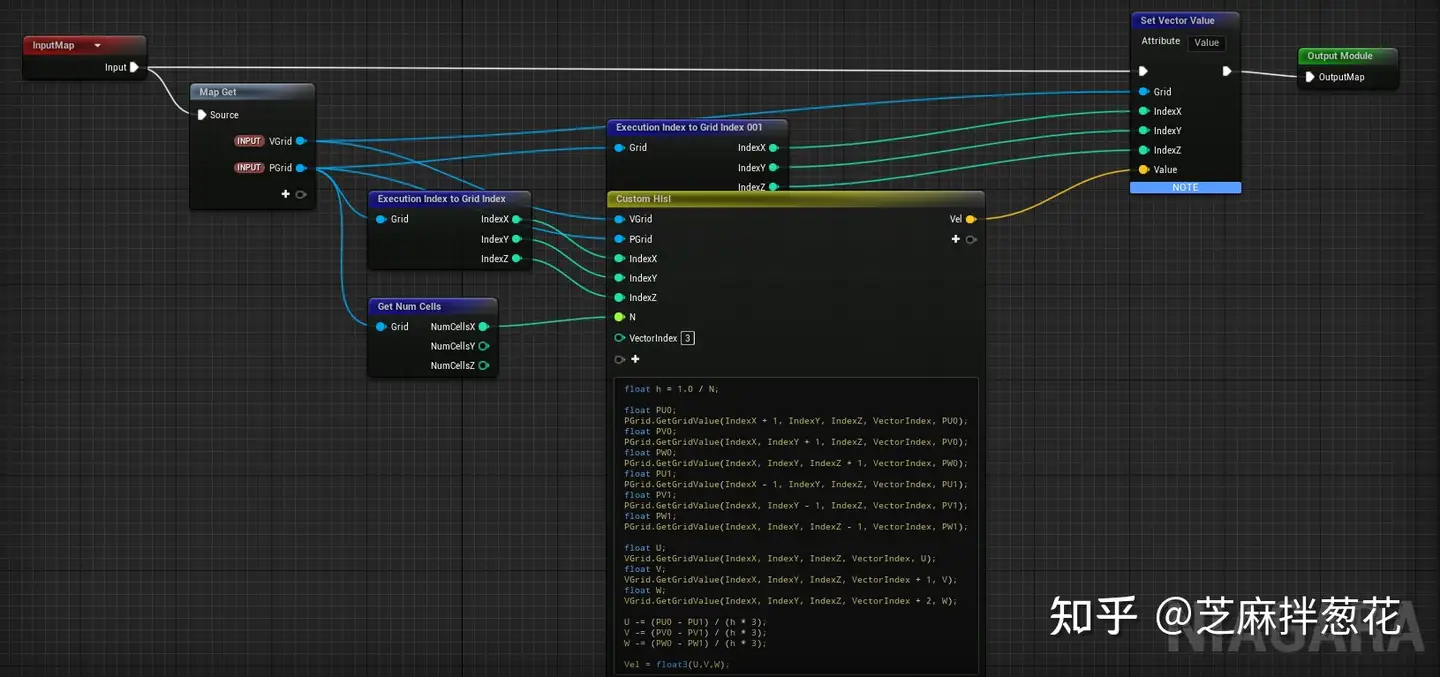
그라디언트를 빼서 속도를 구합니다.
6.국경 문제
네 번의 계산을 통해 보다 사실적인 유체 시뮬레이션을 얻을 수 있지만, 시뮬레이션은 시뮬레이션 상자 내에서만 계산할 수 있으며 캐릭터가 경계를 초과하면 새로운 외부 힘이 들어올 수 없습니다.
이런 종류의 문제에 대한 가장 간단한 해결책은 캐릭터가 경계를 벗어나지 않도록 장면의 크기와 일치하는 시뮬레이션 상자를 만들어 캐릭터가 경계를 벗어나지 않도록 하는 것이지만, 전체 맵을 포함하는 그리드를 정의해야 하지만 필요한 효과는 캐릭터 주변의 작은 영역 내에서만 발생하므로 비용 효율적이지 못합니다.
캐릭터와 일정 거리 내에만 있으면 인터랙티브 바람 효과를 구현할 수 있으므로, 갓 오브 워의 바람 필드를 참고하여 바람 필드 시뮬레이션 박스가 캐릭터의 움직임을 따라가도록 하고 그리드에서 매 프레임마다 바람 필드 정보가 캐릭터의 움직임과 반대 방향으로 오프셋을 수행하여 전체 맵에 인터랙티브 바람 필드 효과를 구현하는 데 소량의 고정 소비량만 필요하도록 할 수 있습니다.

float x = IndexX + Veloctiy.x;
float y = IndexY + Veloctiy.y;
float z = IndexZ + Veloctiy.z;
int x0 = int(x);
int y0 = int(y);
int z0 = int(z);
float x1 = x0 + 1;
float y1 = y0 + 1;
float z1 = z0 + 1;
float xd = (x - x0) / (x1 - x0);
float yd = (y - y0) / (y1 - y0);
float zd = (z - z0) / (z1 - z0);
float VX000;
Grid.GetGridValue(x0, y0, z0, VectorIndex, VX000);
float VX100;
Grid.GetGridValue(x1, y0, z0, VectorIndex, VX100);
float VX010;
Grid.GetGridValue(x0, y1, z0, VectorIndex, VX010);
float VX001;
Grid.GetGridValue(x0, y0, z1, VectorIndex, VX001);
float VX101;
Grid.GetGridValue(x1, y0, z1, VectorIndex, VX101);
float VX011;
Grid.GetGridValue(x0, y1, z1, VectorIndex, VX011);
float VX110;
Grid.GetGridValue(x1, y1, z0, VectorIndex, VX110);
float VX111;
Grid.GetGridValue(x1, y1, z1, VectorIndex, VX111);
float VY000;
Grid.GetGridValue(x0, y0, z0, VectorIndex + 1, VY000);
float VY100;
Grid.GetGridValue(x1, y0, z0, VectorIndex + 1, VY100);
float VY010;
Grid.GetGridValue(x0, y1, z0, VectorIndex + 1, VY010);
float VY001;
Grid.GetGridValue(x0, y0, z1, VectorIndex + 1, VY001);
float VY101;
Grid.GetGridValue(x1, y0, z1, VectorIndex + 1, VY101);
float VY011;
Grid.GetGridValue(x0, y1, z1, VectorIndex + 1, VY011);
float VY110;
Grid.GetGridValue(x1, y1, z0, VectorIndex + 1, VY110);
float VY111;
Grid.GetGridValue(x1, y1, z1, VectorIndex + 1, VY111);
float VZ000;
Grid.GetGridValue(x0, y0, z0, VectorIndex + 2, VZ000);
float VZ100;
Grid.GetGridValue(x1, y0, z0, VectorIndex + 2, VZ100);
float VZ010;
Grid.GetGridValue(x0, y1, z0, VectorIndex + 2, VZ010);
float VZ001;
Grid.GetGridValue(x0, y0, z1, VectorIndex + 2, VZ001);
float VZ101;
Grid.GetGridValue(x1, y0, z1, VectorIndex + 2, VZ101);
float VZ011;
Grid.GetGridValue(x0, y1, z1, VectorIndex + 2, VZ011);
float VZ110;
Grid.GetGridValue(x1, y1, z0, VectorIndex + 2, VZ110);
float VZ111;
Grid.GetGridValue(x1, y1, z1, VectorIndex + 2, VZ111);
float3 V000 = float3(VX000,VY000,VZ000);
float3 V100 = float3(VX100,VY100,VZ100);
float3 V010 = float3(VX010,VY010,VZ010);
float3 V001 = float3(VX001,VY001,VZ001);
float3 V101 = float3(VX101,VY101,VZ101);
float3 V011 = float3(VX011,VY011,VZ011);
float3 V110 = float3(VX110,VY110,VZ110);
float3 V111 = float3(VX111,VY111,VZ111);
//三线性差值
value = V000 * (1 - xd) * (1 - yd) * (1 - zd) +
V100 * xd * (1 - yd) * (1 - zd) +
V010 * (1 - xd) * yd * (1 - zd) +
V001 * (1 - xd) * (1 - yd) * zd +
V101 * xd * (1 - yd) * zd +
V011 * (1 - xd) * yd * zd +
V110 * xd * yd * (1 - zd) +
V111 * xd * yd * zd;
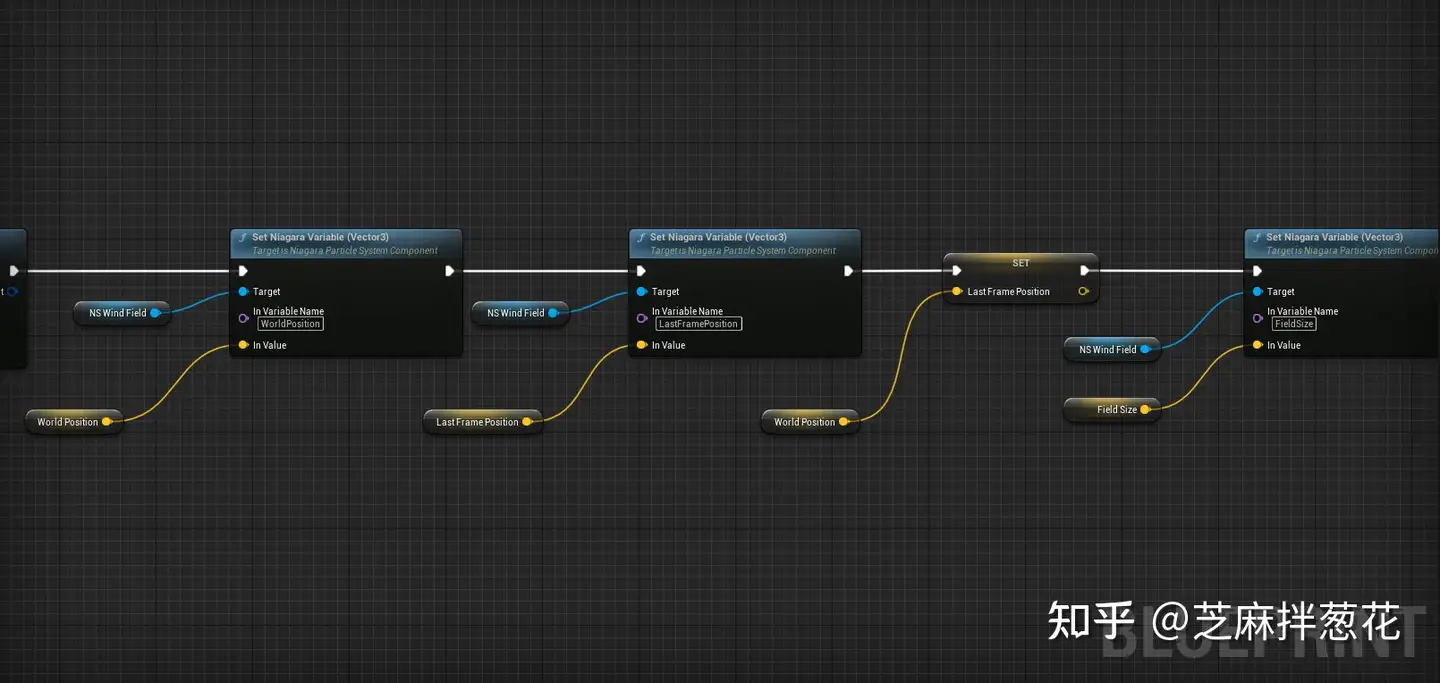
또한 블루프린트에서 실시간으로 위치를 캐릭터 위치로 설정하고 WorldPosition(캐릭터 월드 위치), LastFramePosition(이동 오프셋 계산을 위한 마지막 프레임 위치), FieldSize(시뮬레이션 프레임 크기) 세 파라미터를 나이아가라에 실시간으로 업데이트해야 하며, 바람 필드의 상대 오프셋은 나이아가라에서 현재 위치와 마지막 프레임 위치의 보간을 기반으로 수행합니다. 바람 필드의 상대적 오프셋은 나이아가라에서 현재 위치와 이전 프레임 위치의 보간을 기반으로 수행됩니다.
이 단계는 전체 오프셋을 기준으로 속도를 사용한다는 점을 제외하면 실제로는 반라그랑지안 방식으로 진행 항을 구하는 것과 매우 유사합니다.
이를 통해 캐릭터의 움직임을 따라가는 시뮬레이션 박스를 제공하고, 시뮬레이션 박스 내에서 계산 소비를 제어하며 그 이상은 계산에 관여하지 않습니다.
7.풍력 발전 단지 샘플링

그런 다음 RT_Data라는 1x3 크기의 RT를 정의하고, 여기서 RT 초기화 및 기타 작업은 위의 RT_WindField와 일치하며, RT_WindField 설정을 참조한 다음 바람 필드 컴포넌트의 위치(위 단계의 블루프린트에서 WorldPosition), 바람 시뮬레이션 프레임의 크기(FieldSize) 및 해상도를 각각 세 픽셀에 씁니다. 그런 다음 바람장 컴포넌트의 위치(위 단계의 블루프린트에서 WorldPosition), 바람장 시뮬레이션 프레임의 크기(FieldSize), 해상도를 세 픽셀에 쓰고, RT_Data>는 일종의 커스터마이징된 구조로 해석할 수 있으며, 향후 다른 파티클 시스템에서 바람장을 샘플링하기 위해 실시간 업데이트된 파라미터를 제공하는 데 사용됩니다.

RT_Data가 작성되면 다음 단계는 각 픽셀의 중심값의 RT를 읽는 것으로, 3픽셀만 읽는 경우 세 값의 RT를 얻게 되며, 위치, 크기, 해상도를 가져오는 숫자가 있는 NFS_ParseWindFieldData라는 이름의 나이아가라 함수 스크립트를 정의했습니다.


다른 파티클 시스템에서 파티클 모션을 구동하기 위한 외부 힘으로 바람 필드 RT의 값을 샘플링하기 위해 NMS_WindForce라는 이름의 나이아가라 모듈 스크립트를 만듭니다. 새 나이아가라에서 분수 파티클 이미터를 생성하고 NMS_WindForce 모듈로 드래그한 다음 RT_Data, RT_WindField 및 해상도를 설정합니다.

파티클이 바람의 영향을 받아 캐릭터가 움직이는 방향으로 움직인다는 것을 알 수 있습니다.
마찬가지로 화살표 파티클 매트릭스를 생성하고 바람 필드를 샘플링하여 얻은 결과를 화살표 방향으로 사용하면 바람의 방향을 시각적으로 나타낼 수 있습니다.
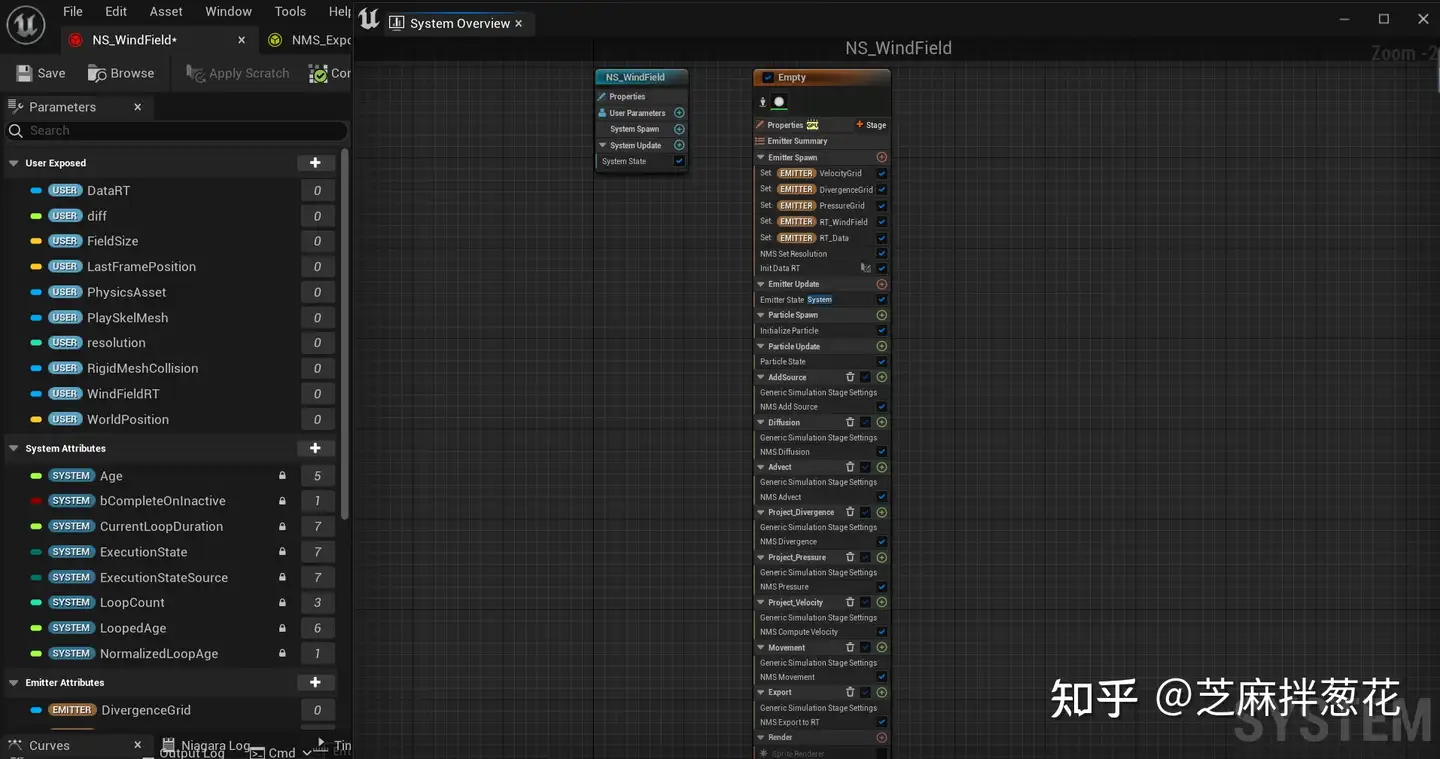
전체 개요
이 글의 길이 때문에 이것은 인터랙티브 바람 필드의 가장 간단한 데모에 불과하며 바람 필드의 응용에는 바람과 초목, 바람과 연기, 바람과 직물 등의 상호 작용도 포함됩니다 (여기서는 구멍을 파기 위해 = = =) 자세한 내용은 다음 글에서 소개하겠습니다.
참고:
知乎 - 安全中心
即将离开知乎 您即将离开知乎,请注意您的帐号和财产安全。 https://developer.nvidia.com/gpugems/gpugems/part-vi-beyond-triangles/chapter-38-fast-fluid-dynamics-simulation-gpu
link.zhihu.com
知乎 - 安全中心
即将离开知乎 您即将离开知乎,请注意您的帐号和财产安全。 https://www.bilibili.com/video/BV1ZK411H7Hc/
link.zhihu.com
你似乎来到了没有知识存在的荒原 - 知乎
知乎,中文互联网高质量的问答社区和创作者聚集的原创内容平台,于 2011 年 1 月正式上线,以「让人们更好的分享知识、经验和见解,找到自己的解答」为品牌使命。知乎凭借认真、专业、友
zhuanlan.zhihu.com
Python: 半拉格朗日格式求解对流方程
话说流体的仿真分为两种观点,其一为欧拉的观点,将流体看作场,关注的是场的物理量,比如在某个位置上有多大的速度,比如前前篇求解NS方程的SIMPLE法,又比如前篇求解对流方程的方法: 派
zhuanlan.zhihu.com
线性方程组-迭代法 2:Jacobi迭代和Gauss-Seidel迭代
0 迭代格式构造本文语境下的 A 一般指非奇异的大规模稀疏矩阵,否则迭代法相较于直接法就没了优势。迭代格式决定了迭代法的收敛性、计算性能。首先把 Ax=b 改写: A x-b=0 \Leftrightarrow x=x-C *(A
zhuanlan.zhihu.com
원문
https://zhuanlan.zhihu.com/p/616999277
【UE5 模拟交互篇】(一)可交互流体风场实现
一.原理介绍1.思路分析先来说观察介质模拟的两种视角:拉格朗日视角跟欧拉视角 拉格朗日视角一般将介质视为粒子(或微小网格)的集合,粒子会随着介质一起移动,通过计算每个粒子的运动
zhuanlan.zhihu.com
'TECH.ART.FLOW.IO' 카테고리의 다른 글
| [번역] UE5 시뮬레이션 인터랙션 챕터] (2) 얕은 물 방정식을 기반으로 인터랙티브 수면 구현하기 (4) | 2024.05.02 |
|---|---|
| [번역] 미호요 스타레일 바텐딩 효과(레이어드 액체 병) 복제 시도 (2) | 2024.05.02 |
| [번역] 팀 개발에서의 Git 운용 예. 언리얼 엔진 (6) | 2024.04.30 |
| [번역] 언리얼 엔진 4 (UE4)/UE5 의 밉 - 커스텀 텍스처 그룹 만들기 (0) | 2024.04.28 |
| [번역] Hierarchical-Z map based occlusion culling ( Old Post ) (0) | 2024.04.23 |
