저자

一.아이디어 분석
게임에서 물과 상호작용하는 일반적인 관행부터 시작하겠습니다:
1.텍스처 애니메이션
일반적으로 여러 개의 리플 텍스처를 실시간으로 RT로 그린 다음 시간에 따라 리플 텍스처의 크기를 순차적으로 조정하여 물결 확산 효과를 시뮬레이션하는 방식으로 수행됩니다. 이것은 일반적으로 사용되는 모바일 인터랙티브 워터 실습이며, 장점은 오버 헤드가 낮고 프로세스가 간단하며 아트에서 제공하는 재료와 매개 변수 조정에 따라 좋은 효과를 얻을 수 있다는 것입니다. 단점은 텍스처의 단순한 애니메이션이기 때문에 효과가 너무 단일하고 반복적이며 아트 리소스에 대한 의존도가 높기 때문에 파도가 장애물을 만나면 반동하고 파도와 다른 복잡한 효과 사이에 서로 간섭이 많아 상호 작용이 이루어지지 않는다는 것입니다.
2.파동 방정식(수학. 물리학)
Wave equation - Wikipedia
From Wikipedia, the free encyclopedia Differential equation important in physics The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound
en.wikipedia.org
파동 방정식은 파동을 설명하는 2차 편미분 방정식으로, 물리학에서 기계파나 전자기파를 설명하는 데 일반적으로 사용되며, 상호작용으로 발생하는 파동도 자연에서 파동입니다. 게임에서 파동 방정식을 사용하여 상호작용하는 물을 구현하면 보다 사실적인 물결의 움직임 패턴을 시뮬레이션할 수 있을 뿐만 아니라 장애물에 부딪힌 후 반동, 파도와 파도가 겹쳐져 보다 복잡한 물결 효과를 구현할 수 있습니다. 그러나 물의 움직임을 설명하기 위해 파동 방정식을 사용하는 것은 여전히 본질적으로 경험적 공식인 물리적 현상에 맞는 수학적 함수입니다. 어떤 경우에는 수면의 융기된 부분의 부피가 함몰된 부분의 부피와 같지 않아 질량 보존이 이루어지지 않습니다.
3.얕은 물 방정식
Shallow water equations - Wikipedia
From Wikipedia, the free encyclopedia Set of partial differential equations that describe the flow below a pressure surface in a fluid Output from a shallow-water equation model of water in a bathtub. The water experiences five splashes which generate surf
en.wikipedia.org
변동 방정식의 근사 피팅과 달리 얕은 물 방정식은 물리 기반 시뮬레이션으로 보다 현실적인 물의 상호작용 효과를 얻을 수 있습니다. 이 백서의 최종 실현 효과는 다음과 같습니다:
1.방정식 소개
얕은 물 방정식은 얕은 유체를 설명하는 방정식의 집합입니다. 이름에서 알 수 있듯이 "얕은 물" 방정식은 매우 얕고 다른 두 차원보다 훨씬 작으며, 즉 수심이 다른 같은 위치의 모든 물은 수직 방향을 무시하고 동일한 이동 속도를 가지며, 수심이 다른 모든 위치 x는 동일한 이동 속도를 갖습니다. 이 논문에서는 주로 2차원 얕은 물 방정식을 구현하므로 xy 방향의 속도만 고려하면 되고 z 방향의 속도는 동일하게 유지됩니다.
얕은 물 방정식은 특정 경우, 즉 1. 2차원 흐름이 z 방향을 무시하고 2. 마찰은 점성 항이 없는 체적 힘이며 3. 압력은 정수압 분포를 따른다는 조건을 만족하는 생베낭 방정식에서 파생된 방정식입니다. 따라서 2차원 생베낭 방정식이라고도 합니다. 생베낭 방정식은 이전 유체 풍장 구현하기 글에서 소개한 적이 있으니 관심 있으신 분들은 확인해 보시기 바랍니다.
[번역] UE5 시뮬레이션과 상호작용 - (1) 인터랙티브 유체 바람막이의 구현
저자시바마마 부추꽃(인터넷명)一.원칙 소개1.아이디어 분석매체의 시뮬레이션을 바라보는 두 가지 관점, 즉 라그랑주 관점과 오일러 관점부터 살펴보겠습니다. 라그랑주 관점은 일반적으로
techartnomad.tistory.com
2.단순 공제

나비에-스토크스 방정식
나비에-스토크스 방정식은 x 방향을 따라 데카르트 좌표계에서 스칼라 형태를 갖습니다:

여기서 u는 x 방향의 속도, v는 y 방향의 속도, w는 z 방향의 속도, t는 시간, p는 압력, ρ는 물의 밀도, ν는 동점도, fx는 x 방향의 외력입니다.
가정 1: 마찰을 체적 힘으로 간주한다고 가정하면, V 에 포함된 마찰은 0으로 가정할 수 있으며 fx in:

가정 2: 흐름은 2차원이며 z는 무시하고 xy 방향의 변화만 고려합니다:

가정 3: 압력은 정수압 분포와 일치하며 압력 방정식과 일치합니다:

가정 3을 나비에-스토크스 방정식의 압력 항에 대입합니다:

마찰과 중력은 fx에 포함되어 있습니다:

가정 1, 2, 3을 나비에-스토크스 방정식에 대입하여 얕은 물 방정식을 도출합니다:

二.구현 프로세스
1.씬 빌딩

여기서는 후디니에서 산악 지형을 절차적으로 생성하고 베지어 커브로 강의 방향을 제어합니다. 커브를 스윕하여 표면이 강처럼 작동하도록 하고 표면을 마스크로 사용하여 산이 강을 피하여 계곡을 형성하도록 합니다. 서페이스 정점의 탄젠트 정보를 정점 색에 강 방향 파라미터로 써야 한다는 점에 유의하세요. 이 글은 물 상호작용 구현에 초점을 맞추고 있고 지면이 제한되어 있기 때문에 후디니 절차적 지형 섹션은 생략했습니다.

지형을 얻기 위해 UE로 임포트할 HDA를 생성합니다.
2.방정식 풀이
이 백서에서는 얕은 물 방정식을 동적 머티리얼 인스턴스에서 계산하고, 계산 결과를 RT에 기록한 다음, 이 RT를 다음 프레임에서 샘플링하는 방식으로 연속적으로 반복하는 방식으로 계산하는 데 중점을 둡니다. 이는 피우드닌자 유체 플러그인에서 프로세스가 작동하는 방식과 유사합니다.
∙ 다음과 같은 구조로 MF_SWE라는 머티리얼 함수를 만듭니다:

여러 입력 파라미터와 세 개의 커스텀 노드가 있습니다. RT는 반복 계산에서 입력 및 출력해야 하는 RT, 높이는 RT의 종횡비(기본값 1), DeltaTime은 각 프레임 사이의 시간 간격, 해상도는 RT의 해상도, IP0 및 IP1은 두 상호작용 지점(캐릭터의 두 발이 수면에 닿는 위치)의 위치, 크기는 시뮬레이션 범위, 페이드 계수는 소산 계수입니다. 계수입니다. 세 개의 커스텀 노드에 대한 코드는 다음과 같습니다:
//defineparameter 노드 전역 변수를 정의하는 데 사용됩니다.
return 0;
}//컴파일된 생성 함수를 차단하는 사용자 정의 사용자 정의 함수에 사용됩니다.
//함수를 차단한 후 전역 변수를 정의할 수 있습니다.
float _Height;
float _DeltaTime;
float _Fade;
float2 _UV;
float2 _IResolution;
float2 _PlaneSize;
float2 _InteractionPos0;
float2 _InteractionPos1;
Texture2D _Tex;
SamplerState _TexSampler;
void SetParameter(float height,float fade, float2 res,float2 planeSize,Texture2D tex){
_Height = height;
_Fade = fade;
_IResolution = res;
_Tex = tex;
_PlaneSize = planeSize;
//하단 끝을 봉인하지 않아도 컴파일 시 사용자 정의가 자동으로 봉인합니다.
//함수 정의 노드 함수를 정의하는 데 사용됩니다.
_TexSampler = TexSampler;
return 0;
}
#define PI 3.1415927
#define width (_Height*(_IResolution.x/_IResolution.y))
#define nds float3(float2(width,_Height)/_IResolution.xy,0)//单位距离
#define bump(r) (cos(1.8483*(r))*exp(-(r)*(r)))//用于交互时产生震荡
//샘플 버퍼
float2 getflag(float2 xy){
float w = _Tex.Sample(_TexSampler,(xy)/(float2(width,_Height))).w;
float fx = (w > 0.375 && w < 0.625 || w > 0.865)? 1 : -1;
float fy = (w > 0.625 && w < 0.865 || w > 0.865)? 1 : -1;
return float2(fx,fy);
}
float getH(float2 xy) {
return _Tex.Sample(_TexSampler,(xy)/(float2(width,_Height))).x*((xy).x<=0.||(xy).x>=width || (xy).y<=0.||(xy).y>=_Height? 0.:1.);
}
float getU(float2 xy) {
return (_Tex.Sample(_TexSampler,(xy)/(float2(width,_Height))).y*((xy).x<=0.||(xy).x>=width? 0.:1.) - 0.5) * 2 ;
}
float getV(float2 xy) {
return (_Tex.Sample(_TexSampler,(xy)/(float2(width,_Height))).z*((xy).y<=0.||(xy).y>=_Height? 0.:1.) - 0.5) * 2 ;
}
float4 SWE(float2 uv,float2 ip0,float2 ip1,float dt){
_DeltaTime = dt;
float2 xy = uv;
const float h0 = 0.5; // 수면의 평균 높이 (m)
const float g = 9.8; // 중력 가속도 (m/s²)
const float f = .001; // 힘의 계수 (rad/s)
const float k = 0.1; // 속도 점성 항력
const float nu = .001; // 동점도 (m²/s), 1e-6
//주변 픽셀의 높이 샘플링
float h = getH(xy);
float hx1 = getH(xy + nds.xz);
float hx0 = getH(xy - nds.xz);
float hy1 = getH(xy + nds.zy);
float hy0 = getH(xy - nds.zy);
//높이의 미분을 계산합니다.
float hx = (hx1 - hx0) / (2. * nds.x);
float hy = (hy1 - hy0) / (2. * nds.y);
//주변 픽셀 샘플링 속도
float u = getU(xy);
float v = getV(xy);
float ux1 = getU(xy + nds.xz);
float ux0 = getU(xy - nds.xz);
float uy1 = getU(xy + nds.zy);
float uy0 = getU(xy - nds.zy);
float vx1 = getV(xy + nds.xz);
float vx0 = getV(xy - nds.xz);
float vy1 = getV(xy + nds.zy);
float vy0 = getV(xy - nds.zy);
//计算散度
float ux = (ux1 - ux0) / (2. * nds.x);
float uy = (uy1 - uy0) / (2. * nds.y);
float vx = (vx1 - vx0) / (2. * nds.x);
float vy = (vy1 - vy0) / (2. * nds.y);
//라플라스 연산자 계산
float ulap = (ux1 + ux0 - 2. * u) / (nds.x * nds.x) + (uy1 + uy0 - 2. * u) / (nds.y * nds.y);
float vlap = (vx1 + vx0 - 2. * v) / (nds.x * nds.x) + (vy1 + vy0 - 2. * v) / (nds.y * nds.y);
//위키피디아의 얕은 물 방정식을 참고하여 직접 적용한 방정식은 다음과 같습니다. https://en.wikipedia.org/wiki/Shallow_water_equations#Non-conservative_form
float ht = -h * (ux + vy) - u * hx - v * hy;
float ut = -g * hx - u * ux - v * uy + nu * ulap - k * u + f * v;
float vt = -g * hy - u * vx - v * vy + nu * vlap - k * v - f * u;
float upH = getH(xy + float2(0, 1 / _IResolution.y));
float downH = getH(xy - float2(0, 1 / _IResolution.y));
float rightH = getH(xy + float2(1 / _IResolution.x,0));
float leftH = getH(xy - float2(1 / _IResolution.x,0));
float averageH = (upH + downH + rightH + leftH) / 4;
if (averageH - h > 0.1) {
h = (upH + downH + rightH + leftH + h) / 5;
}
//변동 함수의 계산은 상호작용이 있을 때 섭동을 생성하며, 상호작용이 없을 때의 상호작용 지점은 다음과 같습니다.(0,0)
if (length(ip0) > 0) {
float r = 120. * length(xy - float2(width, _Height) * ip0);
h -= 500. * bump(r) ;
}
if (length(ip1) > 0) {
float r = 120. * length(xy - float2(width, _Height) * ip1);
h -= 500. * bump(r) ;
}
float3 huv = float3(h, u, v);
float3 huvt = float3(ht, ut, vt);
huv += huvt * _DeltaTime;
huv.x -= _Fade;
huv.x = clamp(huv.x,0,1);
huv.y = clamp(huv.y,-1,1);
huv.z = clamp(huv.z,-1,1);
return float4(huv.x,(huv.y / 2) + 0.5,(huv.z / 2) + 0.5,1);
//메인 펀치톤 노드 전역 변수 설정 얕은 물 방정식 계산하기
SetParameter(h,fade,res,size,tex);
return SWE(uv,ip0,ip1,dt);현재 UE 머티리얼 커스텀 함수는 커스텀 노드를 통해서만 코드를 임베드하는 것이 어렵고, 커스텀 노드는 머리와 꼬리의 좋은 함수를 작성하는 데 도움을 준 것과 같기 때문에 코드의 함수만 채우면 됩니다. 이 경우 일반적인 작성 방식에 따르면 UE는 머티리얼 함수를 지원하지만 함수를 사용자 정의 할 수 없지만 호출의 노드 수준에서만 달성 할 수 있습니다.
Unreal Engine4 Custom Function
在ue4的custom节点中正常书写是无法自定自己的函数的。 custom node会自动将Code栏中的代码加入一组花括号写入HLSL中(因为custom node就相当于自己定义的函数了)。 需要在custom直接定义函数时只需
zhuanlan.zhihu.com
다음은 UE 머티리얼 컴파일 규칙에 따라 코드 내에서 함수의 정의를 호출할 수 있도록 오른쪽 대괄호를 밀봉한 다음 커스텀 함수로 미리 작성하는 더 독창적인 방법의 큰 형님에 대한 참조입니다.
세 개의 커스텀 값 중 처음 두 개는 0이고, 마지막 하나는 방정식의 결과이므로 머티리얼 노드에서 합산하여 최종 출력을 만들어야 합니다. 처음 두 반환 값은 의미가 없지만, 이렇게 하는 이유는 UE 머티리얼 에디터에서 최종 출력에 연결된 노드만 컴파일에 참여하고 연결되지 않은 노드는 셰이더에 컴파일되지 않기 때문입니다.

이렇게 머티리얼을 컴파일하고 셰이더 소스 코드를 살펴보니 일부 전역 변수와 커스텀 함수가 셰이더에 작성된 것을 볼 수 있습니다. 개인적으로 셰이더를 Unity에서 직접 작성하는 것만큼 편리하지는 않은 것 같습니다...

방금 만든 머티리얼 함수를 캡슐화하여 블렌드 모드가 반투명인 머티리얼을 만듭니다.
∙ 액터 BP_SWE 유형의 블루프린트를 생성합니다.
∙ 초기화를 위한 Init 함수를 정의합니다. 새 M_SWE를 부모 머티리얼로 사용하여 동적 머티리얼 인스턴스를 생성하고 블루프린트 변수에 저장합니다.

∙ 반복 계산에서 입력 및 출력을 위한 버퍼로 사용할 RT_SWE라는 렌더 타깃을 생성합니다.
∙ 나중에 여러 머티리얼 간에 파라미터를 공유하는 데 사용할 머티리얼 파라미터 세트인 MRC_River를 생성합니다.
블루프린트에서 메시 페이스 시트를 생성하고 시트의 길이와 너비, 사전 설정 해상도를 머티리얼 파라미터 세트에 기록한 다음 동적 머티리얼 인스턴스의 RT 변수로 RT_SWE를 사용합니다. 메시 시트의 길이와 너비는 시뮬레이션 범위의 경계로 사용됩니다.

∙ 매 프레임마다 실행할 함수 Sim을 정의합니다. 계산된 시간 간격 델타타임, 누적된 시간 시간, 캐릭터 발의 월드 위치에서 UV 위치(IP0, IP1), 캐릭터의 위치를 각 프레임에 설정된 머티리얼 파라미터에 씁니다.


DrawMaterialtoRenderTarget을 실행하고, 위에 입력 RT로 쓰고, 반복 계산을 수행합니다.

마지막으로, 디버그용 RT 결과를 출력하는 데 사용할 수 있는 평면 메시를 제공하는 머티리얼을 생성합니다.
3.모션 오프셋
현재 우리의 상호작용은 제한된 범위 내에서만 구현할 수 있으며, 넓은 범위를 구현하는 가장 쉬운 방법은 캐릭터가 경계를 넘지 않도록 강 전체를 포함하는 고정밀 RT를 정의하는 것이지만, 이는 필요한 효과가 캐릭터 주변의 작은 영역 내에서만 발생하고 강 일부만 사각형 RT와 교차하기 때문에 활용도가 너무 낮으므로 매우 비경제적인 방법입니다.
해결책은 시뮬레이션 범위가 캐릭터의 움직임을 따르도록 하면서 시뮬레이션 결과를 캐릭터의 움직임과 반대 방향으로 오프셋하고 마지막으로 월드 위치에 따라 강 머티리얼을 샘플링하여 항상 캐릭터 근처에서만 리플 상호작용 효과가 나타나고 시뮬레이션 범위를 벗어나는 것은 무작위 노이즈의 파동으로 샘플링하는 것입니다.
∙ 시뮬레이션 결과를 오프셋하는 데 사용되는 머티리얼 M_OffsetRT를 생성합니다.

//사용자 정의 노드
return ((xy).x<=0.||(xy).x>=1. || (xy).y<=0.||(xy).y>=1.? 0.:1.);블루프린트 BP_SWE에 캐릭터의 움직임을 따라가는 함수 Move를 생성하고, 두 프레임의 PostionAndLastPosition 전후의 블루프린트 위치를 기록한 다음, PostionAndLastPosition과 방정식 RT의 결과를 위에서 생성한 M_OffsetRT의 다이내믹 머티리얼 인스턴스에 함께 전달하여 오프셋 계산을 수행합니다. 오프셋 계산이 수행됩니다.
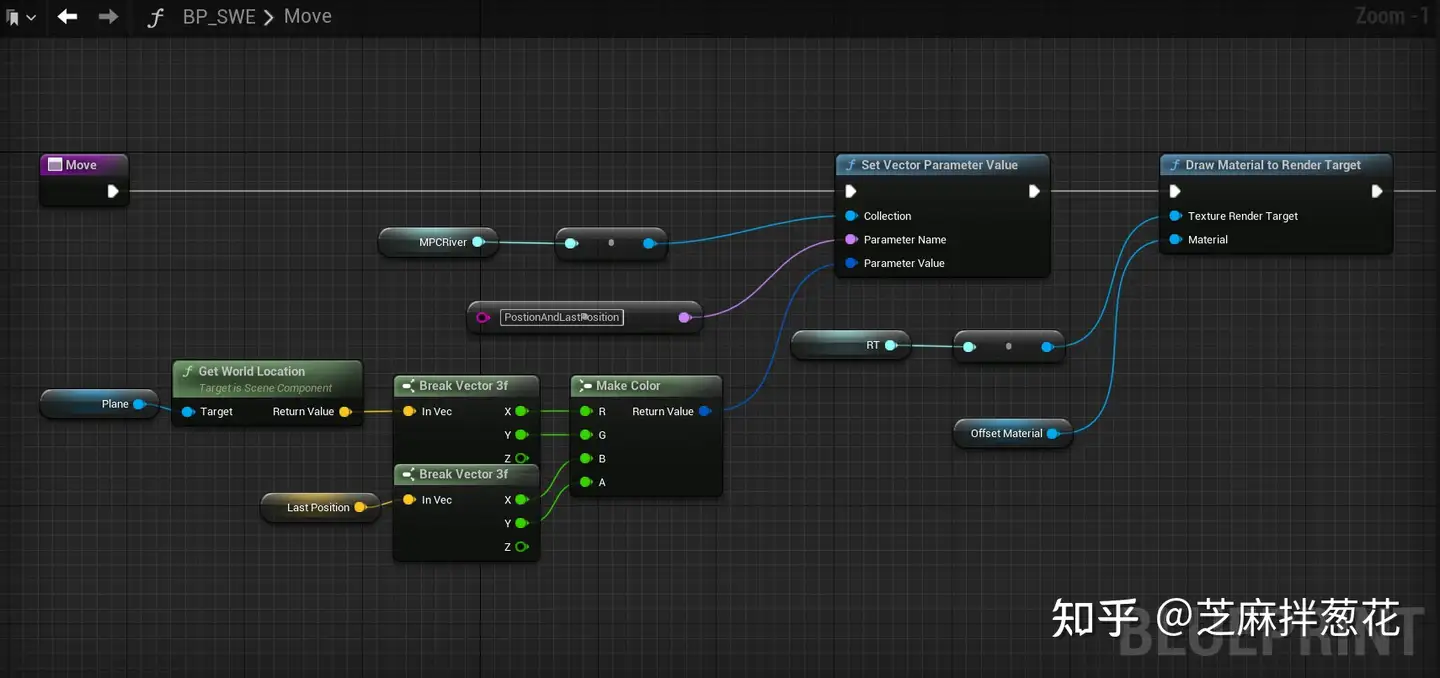


4.강 상호 작용
∙ 강 머티리얼 M_Flow 만들기


거리 블렌딩을 기반으로 수체 색상을 가져와 BaseColor로 출력합니다.

프레넬 계산, 불투명도 출력

버텍스 색상(강 흐름 정보)을 플로우맵 샘플링된 랜덤 노이즈 맵으로 읽고 그 결과를 원거리 수면 파도 높이로 블렌딩합니다.

월드 포지션이 시뮬레이션 박스 범위에 있는 버텍스 위치는 샘플링된 RT 의 UV 공간으로 변환되고, 샘플링된 RT 는 높이를 얻습니다.

높이를 근거리와 원거리, 높이를 노멀로 블렌딩하고 출력을 노멀로 출력합니다.
마지막으로 HDA에서 생성한 강 스태틱 메시 위에 머티리얼을 적용합니다:
레퍼런스
Shallow water equations - Wikipedia
From Wikipedia, the free encyclopedia Set of partial differential equations that describe the flow below a pressure surface in a fluid Output from a shallow-water equation model of water in a bathtub. The water experiences five splashes which generate surf
en.wikipedia.org
Shallow-water wave theory - Coastal Wiki
Introduction This article explains some theories of periodic progressive waves and their interaction with shorelines and coastal structures. The first section provides a descriptive overview of the generation of wind waves, their characteristics, the proce
www.coastalwiki.org
【教学向】从零开始的流体力学(一维浅水方程+有限体积法)
“我喜欢的人是诗人、剑客、哲学家,还是空气动力学的先驱...“笔者其实从三个多月前就萌生了执笔这一篇文章的想法了。只不过笔者因为春季学期太忙,新建了个文件夹之后就把这篇文章一
zhuanlan.zhihu.com
真实感水体渲染技术总结
之前在【GPU精粹与Shader编程】系列中写过一篇 《真实感皮肤渲染技术总结》,这篇文章则是它的番外篇,主要关注于真实感水体渲染技术。本文将对游戏开发以及电影业界的真实感水体渲染技术
zhuanlan.zhihu.com
원문
【UE5 模拟交互篇】(二)基于浅水方程实现交互水面
一.思路分析先来说说游戏中常见的交互水面做法: 1.纹理动画一般是通过实时绘制多张涟漪纹理到RT上,然后随时间先后对涟漪纹理进行缩放,模拟出水波扩散效果。这种是移动端常用的交互水
zhuanlan.zhihu.com
'TECH.ART.FLOW.IO' 카테고리의 다른 글
| [번역]테크니컬 아트 노트 | 언리얼 5 프로시저럴 제너레이션 프레임워크의 기본에 대한 가이드. (0) | 2024.05.14 |
|---|---|
| [번역] UE5 시뮬레이션 상호작용 (3) 단일 패스 헤어 머티리얼 + 바람 필드 상호작용 체계를 달성하기 위한 레이 마칭 디스턴스 필드 (1) | 2024.05.03 |
| [번역] 미호요 스타레일 바텐딩 효과(레이어드 액체 병) 복제 시도 (2) | 2024.05.02 |
| [번역] UE5 시뮬레이션과 상호작용 - (1) 인터랙티브 유체 바람막이의 구현 (1) | 2024.05.01 |
| [번역] 팀 개발에서의 Git 운용 예. 언리얼 엔진 (6) | 2024.04.30 |
