역자의 말: 최근 애픽코리아 언리얼 페스트2024 행사가 마무리 되면서 아마도 더 많은 그래픽스 프로그래머 또는 테크아티스트들은 비지빌리티 버퍼 또는 클러스터드 컬링과 지연 텍스처링등에 대한 더 많은 관심을 갖게 되었을겁니다. 호라이즌 제로던 포비든 웨스트에서 소개 했던 지연 텍스처링 즉 디퍼드 텍스처링에서도 비지빌리티 버퍼와 머티리얼 ID ( 인텔 논문 참조 ) 등을 사용하여 폴리지 렌더링 최적화에 사용 한 케이스도 있으며 나나이트 또한 비지빌리티 버퍼의 하이브리드 형식이라고 할 수 있습니다. 몇 년 전 이미 비지빌리티 버퍼와 머티리얼 그래프 라는 멋진 토픽이 있었고 역시 최근 시그라프 2024에서 비지빌리티 버퍼와(VisBuffer) 가변비율 셰이딩(VRS)에 대해서 자세하게 소개 해 준 존 헤이블 씨의 토픽이었기 때문에 이렇게 소개 하고자 합니다.
저자 : JOHN HABLE @FILMICWORDS

그는 일렉트로닉 아츠, 너티독, 에픽게임즈, 유니티에서 경력을 쌓은 렌더링 프로그래머입니다.

가시성 렌더링의 모험
- Part 1: 머티리얼 그래프를 사용한 비저빌리티 버퍼 렌더링
- Part 2: 디커플링된 가시성 멀티샘플링
- Part 3: 가시성 버퍼 렌더링이 포함된 소프트웨어 VRS(가변비율셰이딩)
- Part 4: 가시성 TAA 및 서브샘플 히스토리를 사용한 업샘플링
소개
지난 1년 정도는 모두에게 이상한 시기였습니다. 우리 모두는 각자의 방식으로 코로나 격리에 대처해 왔고, 제 경우에는 코딩을 해왔습니다. 아시다시피 작은 트라이앵글은 쿼드 사용률 저하 등 여러 가지 이유로 GPU에서 비효율적입니다. 이론적으로 비저빌리티 버퍼는 쿼드 활용도가 낮은 경우 디퍼드보다 더 탄력적이기 때문에 저는 비저빌리티 버퍼 렌더러가 기존 디퍼드 렌더러보다 더 나은 성능을 얻을 수 있을 것이라는 직감을 가지고 있었습니다. 시간이 조금 남아서 이 이론을 테스트하기 위해 Dx12 토이 엔진을 만들었습니다.
개요 및 선행 기술
가시성 버퍼의 개념은 매우 간단합니다. 첫 번째 패스에서 오브젝트와 트라이앵글 ID를 단일 값(일반적으로 패킹된 U32)에 저장하는 '가시성 버퍼'를 렌더링합니다. 그런 다음 이 트라이앵글/오브젝트 ID만 있으면 필요한 매개변수를 가져올 수 있습니다.
최초의 주요 논문은 인텔의 크리스토퍼 번즈와 워렌 헌트가 작성한 것입니다[3].
https://jcgt.org/published/0002/02/04/
jcgt.org
이 논문은 '가시성 버퍼'라는 용어를 만들었을 뿐만 아니라 삼각형 ID를 저장하고 보간된 버텍스 데이터를 재구성하는 최초의 참고 자료였습니다. 여러 머티리얼을 처리하기 위해 화면을 타일로 분할하고 그 안의 픽셀을 분류했습니다. 그런 다음 필요한 픽셀에 닿는 타일에 대해서만 머티리얼당 하나의 드로우 콜을 렌더링했습니다. 가시성 버퍼는 다른 방식으로 렌더링을 최적화하는 데도 사용되었는데, 멀티샘플링 압축 알고리즘으로 이 문제에 접근한 크리스토프 쉬드와 카스텐 닥스바허[12]가 그 예입니다. ConfettiFX의 볼프강 엥겔은 임의의 머티리얼 그래프 대신 바인드리스 텍스처를 사용하는 가시성 버퍼[5]를 시연했습니다. 이 접근 방식은 머티리얼을 임의의 텍스처 액세스가 가능한 하나의 언더셰이더로 취급합니다. 또한 허용된 라이선스에 따라 소스 코드를 제공하므로 관심이 있다면 한 번 살펴보는 것이 좋습니다[4].

물론 가장 최근의 작품은 에픽게임즈의 언리얼 5 나나이트입니다. 과거와는 다른 방식으로 문제에 접근합니다. 제가 알려드릴 비밀은 없지만, 높은 수준의 접근 방식은 공개적으로 알려져 있습니다. 나나이트는 비저빌리티 버퍼를 GBuffer를 대체하는 대신 비저빌리티 버퍼를 최적화하여 GBuffer를 더 효율적으로 생성하는 데 사용하고 있습니다. 특히 GPU 래스터라이저는 작은 트라이앵글에서 성능 비효율이 발생하기 때문에 나나이트는 개요 동영상[7]에서 볼 수 있듯이 커스텀 래스터라이저를 사용하여 이러한 병목 현상을 우회합니다. 1:00:45로 이동하면 트라이앵글 크기에 대한 간략한 설명을 볼 수 있습니다. UE5 비저빌리티 래스터라이저는 나나이트 전용 래스터라이저이므로 다른 오브젝트는 표준 디퍼드 경로를 거칩니다.
이론적으로 비저빌리티 렌더링에는 GBuffer가 필요하지 않습니다. 노멀이 필요한 경우 언제든지 버텍스 파라미터에서 직접 가져올 수 있습니다. 그리고 다시 필요하면 다시 가져올 수 있습니다. 하지만 실제로 머티리얼 그래프는 이미 상당히 길고 매년 점점 더 길어지고 있습니다. 직접 조명만 필요하다면 GBuffer 없이도 할 수 있습니다. 하지만 직접 조명, 스크린 공간 반사, 앰비언트 프로브 등 프레임당 일반적인 여러 번과 같은 값이 필요하므로 머티리얼 출력을 GBuffer에 저장하는 것이 가장 좋은 방법인 것 같습니다.

여기서 제안한 변형에서는 가시성 버퍼를 사용하여 GBuffer를 생성하고 모든 트라이앵글에 사용할 것입니다. 또한 임의의 머티리얼 그래프로 이 작업을 수행할 예정이므로 자체 분석 부분 미분 계산해야 합니다. 이 테스트를 수행하면서 답을 찾으려는 몇 가지 질문이 있습니다:
- 머티리얼 그래프로 분석 부분 미분을 효율적으로 계산할 수 있을까요?
- 다시 말해, 이 접근 방식이 실행 가능할까요? 분석적 부분 파생상품을 계산할 수 없다면 이 접근 방식은 시작도 할 수 없습니다.
- 트라이앵글 수가 매우 많은 경우(트라이앵글당 1픽셀) 가시성 접근 방식이 더 빠릅니까?
- 이 접근 방식이 향후 워크로드에 더 빠를까요? 영화 화질을 구현하려면 결국 모든 트라이앵글의 크기를 1픽셀로 줄여야 합니다. 배경, 캐릭터, 잔디, 소품 등 모든 것을요.
- 보다 일반적인 삼각형 크기(삼각형당 5~10픽셀)는 어떨까요? 이 경우에도 가시성 접근 방식이 더 빠를까요?
- 이 접근 방식이 현재 AAA 게임 워크로드에 더 빠를까요?
아래 테스트에서 세 가지 질문에 대한 정답은 다음과 같습니다: 예! 하지만 이 엔진은 실제 AAA 엔진이 아닌 장난감 엔진이라는 점을 주의하세요.
포워드/디퍼드/가시성(비지빌리티) 개요
먼저 포워드, 디퍼드 및 가시성 렌더링에 대해 간략히 살펴보겠습니다. 포워드 렌더링에서는 단일 픽셀 셰이더에서 모든 것을 계산하며, 다음과 같이 보입니다.
struct Interpolators; // the position, normal, uvs, etc.
struct BrdfData; // normal mapped normal, albedo color, roughness, metalness, etc.
struct LightData; // the output lighting data, usually just a float3
// Pass 0: Render all meshes, output final light color
LightData MainPS(Interpolators interp)
{
BrdfData brdfData = MaterialEval(interp);
LightData lightData = LightingEval(brdfData);
return lightData;
}기본적으로 모든 물리 기반 포워드 셰이더는 코드에 없는 숨겨진 단계에서 시작됩니다:
버텍스 보간입니다. 하드웨어는 버텍스 데이터를 보간하고 보간된 버텍스 데이터를 마술처럼 전달합니다. 물론 하드웨어가 마법을 부리지는 않지만 이 단계는 픽셀 셰이더 코드가 실행되기 전에 이루어집니다. 다음 단계에서는 MaterialEval() 함수가 보간된 값(UV, 노멀, 탄젠트 등)을 사용하여 수학 및 텍스처 룩업을 수행하여 표면 머티리얼 파라미터를 계산합니다. 여기에는 일반적으로 노멀 매핑된 노멀, 기본 색상 등이 포함됩니다. 마지막 단계에서는 이러한 매개변수에 대해 모든 조명을 평가하고 결과 색상을 출력합니다.
그러나 요즘 게임에서 렌더링하는 데 더 일반적인 접근 방식은 두 번의 패스로 렌더링하는 GBuffer를 사용하는 디퍼드입니다.
// Pass 0: Render all meshes, output material data.
BrdfData MaterialPS(Interpolators interp)
{
BrdfData brdfData = MaterialEval(interp);
return brdfData;
}
// Pass 1: Compute shader (or large quad) to calculate lighting.
LightData LightingCS(float2 screenPos)
{
BrdfData brdfData = FetchMaterial(screenPos);
LightData lightData = LightingEval(brdfData);
return lightData;
}디퍼드 접근 방식은 포워드와 동일한 기본 단계를 사용합니다. 그러나 조명 데이터는 전체 화면 쿼드 또는 컴퓨팅 셰이더와 같은 별도의 패스에서 평가됩니다. 장점은 다음과 같습니다:
- 가장 큰 장점은 조명 함수가 픽셀당 정확히 한 번만 실행되도록 보장된다는 것입니다. 지오메트리를 래스터화할 때 MaterialPS()는 픽셀당 두 번 이상 실행될 수 있지만 LightingCS()는 한 번만 실행되도록 보장됩니다.
- MaterialEval() 함수와 LightingEval() 함수가 같은 셰이더에 있으면 둘 다 최악의 레지스터 할당으로 컴파일되는 반면, 분리되어 있으면 한 패스가 다른 패스보다 적은 수의 레지스터를 사용할 수 있고 더 나은 점유를 달성할 수 있습니다.
- 디퍼드 접근 방식을 사용하면 화면 공간 반사, SSGI, SSAO 및 서브서피스 스캐터링과 같은 다른 이펙트에 사용할 수 있는 GBuffer가 있습니다.
분명한 단점은 디퍼드를 사용하면 대역폭 사용량이 증가한다는 것입니다. 일반적으로 화면 공간 효과와 향상된 셰이더 성능이 대역폭과 메모리 비용을 크게 능가합니다. 물론 MSAA가 꼭 필요하다면 모든 것이 달라지겠지만 이는 완전히 다른 이야기입니다.
가시성 렌더링은 매우 다른 접근 방식을 취합니다. 가시성은 조명 색상(예: Forward)이나 GBuffer 데이터(예: Deferred)를 래스터화하는 대신 삼각형과 그리기 호출에 대한 ID만 래스터화합니다. 이심좌표(바리센트릭 좌표)나 도함수(미분)를 저장할 수도 있지만, 여기서는 단일 삼각형 ID를 사용하겠습니다.
// Pass 0: Rasterize all meshes, just output thin visibility
U32 VisibilityPS(U32 drawCallId, U32 triangleId)
{
return (drawCallId << NUM_TRIANGLE_BITS) | triangleId;
}
// Pass 1: In a CS convert from triangle ID to BRDF data
BrdfData MaterialCS(float2 screenPos)
{
U32 drawCallId = FetchVisibility() >> NUM_TRIANGLE_BITS;
U32 triangleId = FetchVisibility() & TRIANGLE_MASK;
Interpolators interp = FetchInterpolators(drawCallId, triangleId);
BrdfData brdfData = MaterialEval(interp);
return brdfData;
}
// Pass 2: In a CS, fetch BRDF data and calculate lighting
LightData LightingCS(float2 screenPos)
{
BrdfData brdfData = FetchMaterial(screenPos);
LightData lightData = LightingEval(brdfData);
return lightData;
}머티리얼과 라이팅 단계는 별도의 패스를 사용하며, 이는 대부분의 선행 기술과는 다릅니다 [3,13]. 대부분의 이전 논문에서는 GBuffer 대역폭을 줄이기 위해 두 단계를 함께 수행했습니다. 하지만 머티리얼 셰이더의 복잡성을 고려할 때 GBuffer가 필요하다는 것이 제 생각입니다. 머티리얼 셰이더는 테크아트적인 이유로 인해 길어질 수 있습니다.
아티스트가 만든 머티리얼 셰이더는 비효율적일 수 있습니다(약간 과장된 표현일 수도 있습니다). 하지만 완전히 엉망인 경우에도 머티리얼이 달성하고자 하는 효과에는 대개 타당한 이유가 있으며, 그 효과가 가장 성능이 좋은 방식으로 달성되지 않더라도 그 이유가 있습니다. 제 개인적인 견해는 긴 머티리얼 그래프는 앞으로도 계속 유지될 것이며, 비용이 많이 들 것이므로 이를 처리하는 가장 효율적인 방법을 찾아야 한다는 것입니다.
그렇다면 여러 머티리얼, 특히 머티리얼 그래프를 어떻게 처리할 수 있을까요? 아래 플로우 다이어그램을 사용하겠습니다.
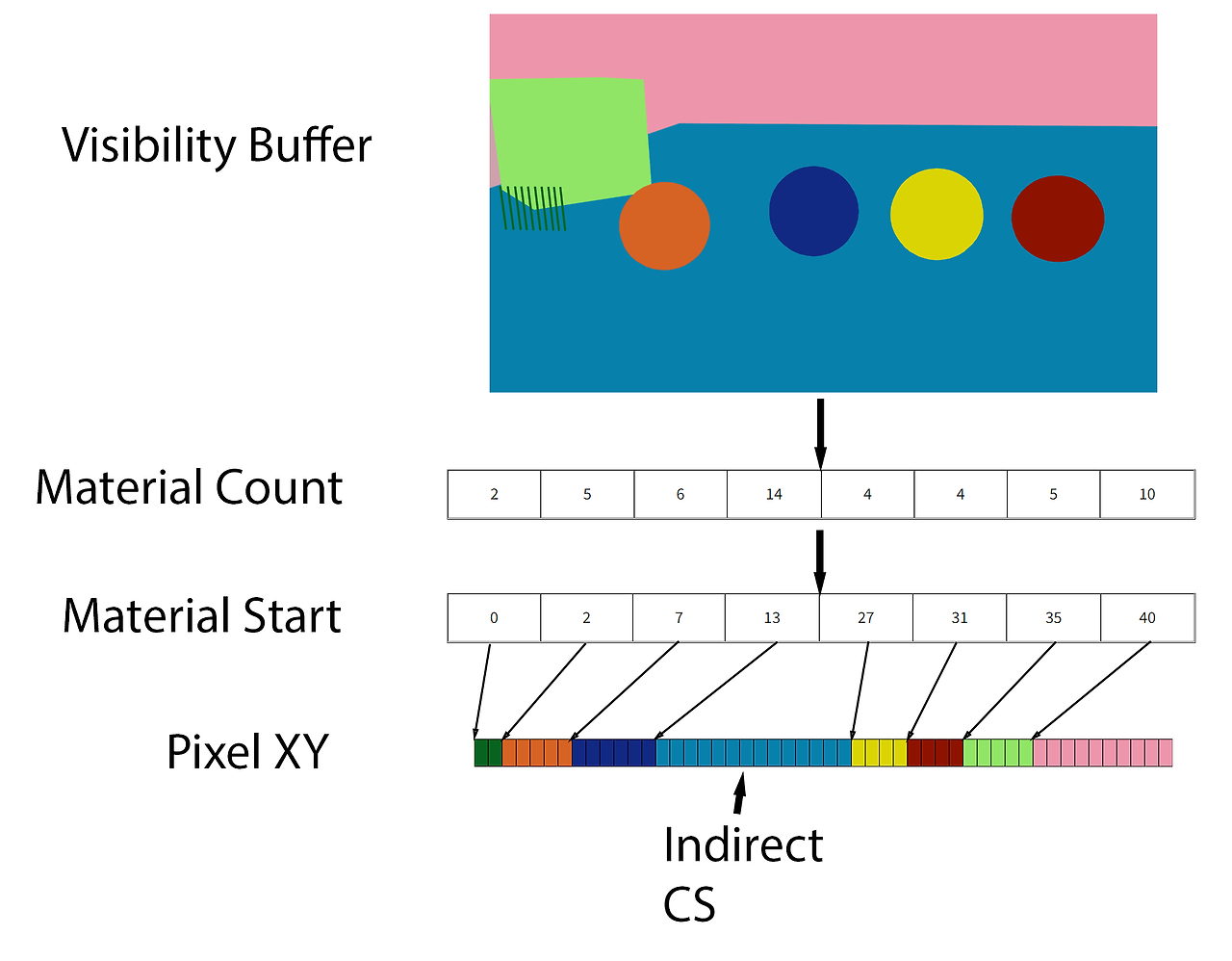
- 첫 번째 단계로 전체 화면 가시성 버퍼를 렌더링합니다.
- 각 픽셀을 살펴보고 각 머티리얼에 사용된 픽셀 수를 계산합니다. 결과를 머티리얼 수 버퍼에 저장합니다.
- 접두사 합계를 수행하여 머티리얼 시작을 파악합니다.
- 가시성 버퍼를 통해 다른 패스를 실행하여 각 픽셀의 XY 위치를 픽셀 XY 버퍼의 적절한 위치에 저장합니다. 픽셀 XY 버퍼에는 가시성 버퍼와 동일한 수의 요소가 있다는 점에 유의하세요.
- 각 머티리얼에 대해 간접 계산 셰이더를 실행하여 GBuffer 데이터를 계산합니다.
이것이 패스가 정렬되는 방식이며, 이를 통해 생성된 HLSL 코드가 다른 여러 머티리얼 그래프를 렌더링할 수 있습니다. 하지만 GBuffer 데이터를 계산할 때 해결해야 할 문제가 하나 더 있습니다: 부분 도함수 입니다.
하드웨어 부분 파생물
픽셀 셰이더를 작성했다면 어느 시점에서 텍스처에서 읽을 줄을 작성해 본 적이 있을 것입니다. 이런 식으로요:
Sampler2D sampler;
Texture2D texture;
...
float2 uv = SomeUv();
float4 value = texture.Sample(sampler,uv);이 코드를 실행하면 GPU가 최적의 밉맵 레벨을 파악하여 데이터를 읽고 필터링합니다. 하지만 올바른 밉맵 레벨을 어떻게 알아낼까요?
핵심은 픽셀 셰이더가 단일 픽셀에서 실행되지 않는다는 것입니다. 그 대신 쿼드라고 하는 2x2 픽셀 그룹에서 실행됩니다. 아래 보라색 예시에서 삼각형은 4개의 픽셀을 모두 포함하며, 4개의 픽셀은 모두 동일한 셰이더를 락스텝으로 실행하고 텍스처를 읽는 동안 GPU는 4개의 UV 값을 비교하여 밉맵 레벨을 결정합니다. GPU는 오른쪽 픽셀에서 왼쪽 픽셀을 빼서 부분 미 x를, 아래쪽에서 위쪽을 빼서 부분 미분 y를 추정할 수 있습니다. 그런 다음 그 차이의 로그2에서 적절한 레벨을 결정할 수 있습니다. 이 접근 방식을 유한 차이라고 합니다.
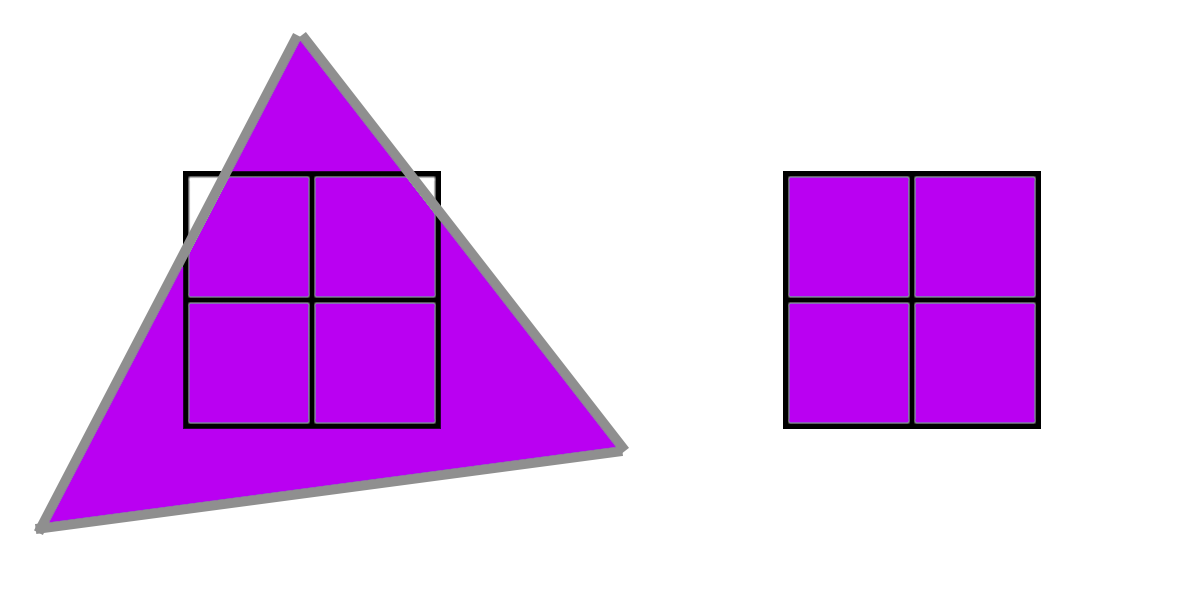
하지만 아래 삼각형처럼 삼각형이 4개의 픽셀을 모두 덮지 않고 3개의 픽셀만 덮는 경우에는 어떻게 될까요? 이 경우 GPU는 누락된 픽셀에 삼각형을 추정하여 평소처럼 실행합니다. 실제로 실행되는 3개의 픽셀을 "활성 레인"이라고 하고, 나머지 3개의 픽셀에 파생물을 제공하기 위해 실행되는 1개의 픽셀을 "헬퍼 레인"이라고 합니다.

자세한 내용은 HLSL 셰이더 모델 6.0 웨이브 내재성 문서 [9]를 참조하세요. 실제로 동일한 2x2 쿼드에 있는 다른 픽셀 사이에 데이터를 전달할 수 있는 고유성이 있습니다. 하지만 여러 개의 삼각형이 동일한 2x2 쿼드에 겹치면 어떻게 될까요?
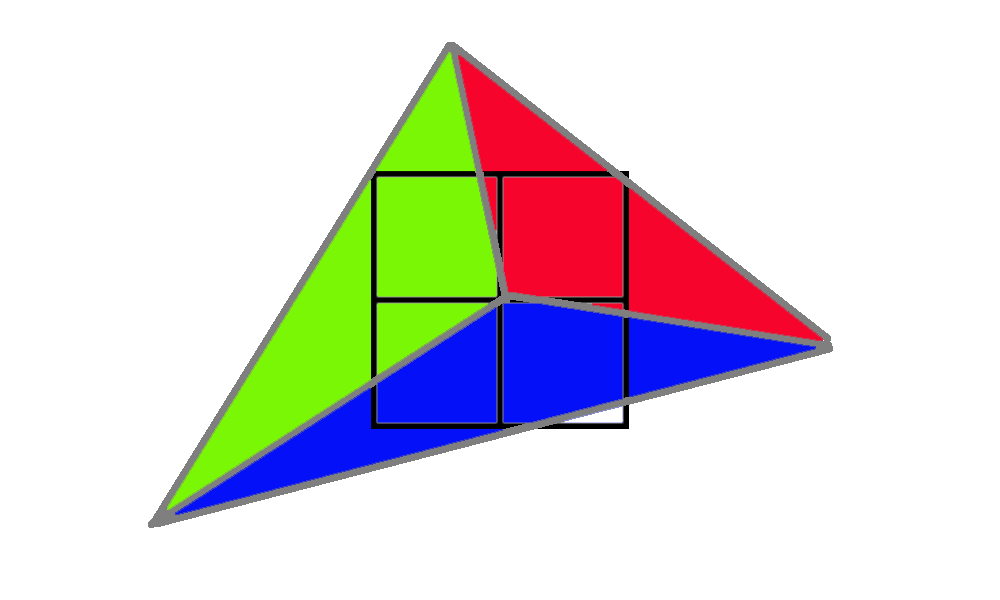
이 샘플에서는 3개의 서로 다른 삼각형이 2x2 그리드에서 샘플 중심을 덮고 있습니다. 먼저 녹색 삼각형은 왼쪽 상단 모서리를 덮고 있습니다. 이를 렌더링하기 위해 GPU는 왼쪽 상단 픽셀을 활성 레인으로 렌더링하고 나머지 세 개는 헬퍼 레인으로 음영 처리하여 하나의 활성 레인에 텍스처 파생물을 제공합니다.

다음으로 파란색 삼각형은 2개의 활성 레인과 2개의 헬퍼 레인을 갖습니다.
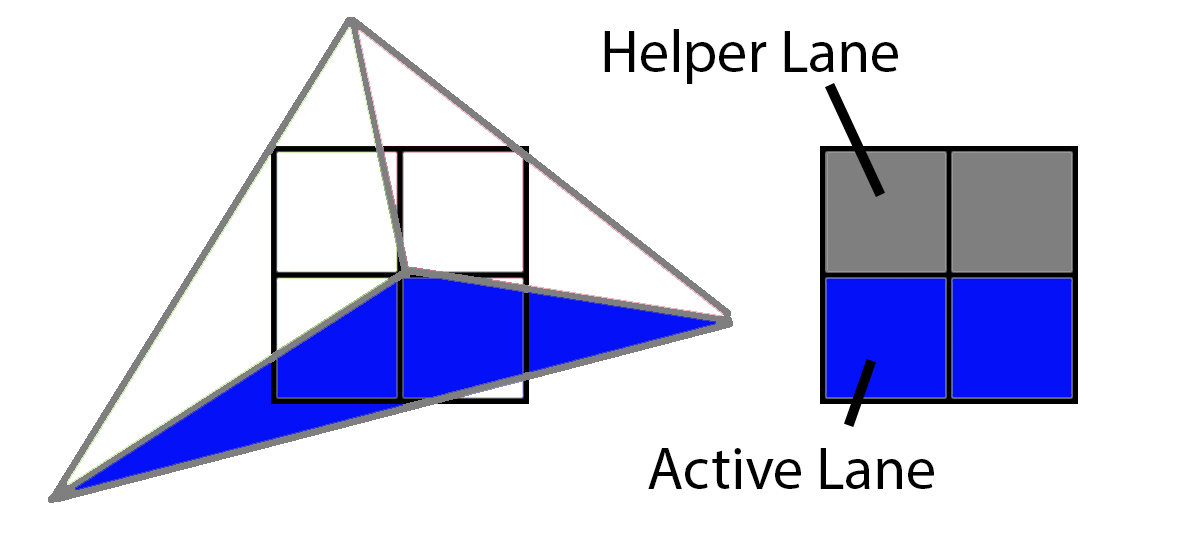
마지막으로 빨간색 삼각형은 활성 레인 1개와 헬퍼 레인 3개를 갖습니다.

쿼드에 4개의 픽셀을 모두 포함하는 트라이앵글 1개가 있는 경우 픽셀 셰이더 워크로드는 다음과 같습니다:

하지만 쿼드에 4개의 픽셀을 덮는 3개의 트라이앵글이 있는 경우 픽셀 셰이더 워크로드는 다음과 같습니다:

동일한 2x2 쿼드를 커버하는 3개의 트라이앵글이 있다면 실제로는 4개의 픽셀을 모두 커버하는 단일 트라이앵글에 비해 3배의 픽셀 셰이더 작업을 수행해야 합니다. 활성 레인을 총 레인으로 나눈 비율을 쿼드 활용률이라고 합니다. 보라색 쿼드는 쿼드 사용률이 100%이지만 이 세 개의 삼각형의 워크로드는 쿼드 사용률이 33%입니다. 쿼드 사용률에 영향을 미치는 주요 요인은 무엇일까요? 삼각형 크기입니다.
쿼드 활용 효율성
이를 감안하여 1픽셀 트라이앵글만 렌더링한다고 가정해 보겠습니다. 오버드로가 없더라도 각 2x2 쿼드에는 1개의 활성 레인과 3개의 헬퍼 레인이 있습니다.

전체 씬을 1픽셀 트라이앵글로 렌더링하려면 각 픽셀 셰이더를 한 번이 아니라 픽셀당 4번 실행해야 합니다. 포워드 및 디퍼드 머티리얼 셰이더는 모든 픽셀에 대해 4번 실행되는 반면, 디퍼드 조명 및 비저빌리티 머티리얼과 조명 패스는 픽셀당 한 번만 실행됩니다.
1픽셀 크기의 트라이앵글에 대한 픽셀당 셰이더 함수 호출 수입니다:
MaterialLighting
| Material | Lighting | |
| Forward | 4x | |
| Deferred | 4x | 1x |
| Visibility | 1x | 1x |
다른 극단으로 나아가서 커어다란 삼각형이 있다면 어떻게 될까요? 이 경우 훨씬 더 간단합니다. 헬퍼 레인의 수는 렌더링되는 전체 픽셀의 작은 비율이며, 이 글의 목적상 부수적이라고 할 수 있습니다. 픽셀 셰이더는 픽셀당 한 번 정도 실행됩니다.

큰 트라이앵글의 픽셀당 대략적인 셰이더 함수 호출 수입니다:
MaterialLighting
| Material | Lighting | |
| Forward | 1x | |
| Deferred | 1x | 1x |
| Visibility | 1x | 1x |
이것이 극단적인 경우라면 중간은 어떻게 될까요? 중간은 더 복잡합니다. 일반적으로 삼각형당 약 10픽셀을 목표로 하는 것이 일반적입니다. 10픽셀 삼각형의 쿼드 활용도는 어느 정도일까요? 모양에 따라 다르겠지만 몇 가지를 시도해보고 알아봅시다. 가장 간단한 10픽셀 삼각형부터 시작하겠습니다.
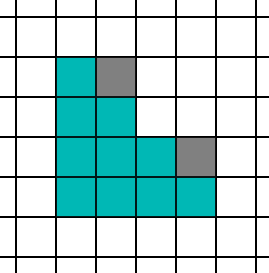
언뜻 보기에는 활성 레인이 10개이고 헬퍼 레인은 2개뿐이므로 정말 좋아 보입니다. 하지만 이 삼각형이 2x2 그리드에 정렬될 수 있는 방법은 4가지가 있습니다.
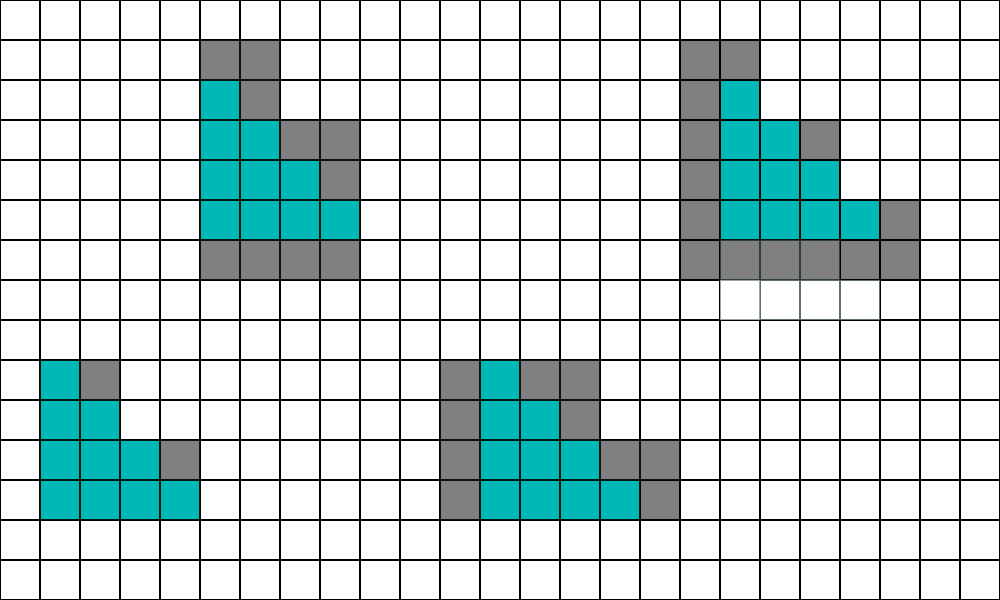
계산을 해보면 평균적으로 10개의 활성 레인에 9개의 헬퍼 레인이 있습니다. 다음으로 조금 더 길고 얇은 것을 사용해 보겠습니다.

이 형태에서는 활성 레인 10개에 평균 11개의 헬퍼 레인이 있습니다. 다음은 최악의 경우의 모양입니다:

제가 정확하게 세어본다면 헬퍼 레인 21개와 액티브 레인 10개입니다(아아). 삼각형이 완벽하게 정렬되어야 이런 모양을 만들 수 있기 때문에 극단적인 경우입니다. 합리적인 추정치로 첫 번째(청록색) 및 두 번째(주황색) 삼각형은 동일하게 발생하고 세 번째(보라색) 삼각형은 발생하지 않는다고 가정하면 쿼드 사용률이 50%에 도달합니다. 즉, 포워드 및 디퍼드 머티리얼 패스는 픽셀당 약 2배로 실행됩니다. 다시 한 번, 디퍼드 라이팅과 비저빌리티 머티리얼 및 라이팅은 픽셀당 한 번 실행됩니다.
10픽셀 트라이앵글의 픽셀당 대략적인 셰이더 함수 호출 수입니다:
MaterialLighting
| Material | Lighting | |
| Forward | 2x | |
| Deferred | 2x | 1x |
| Visibility | 1x | 1x |
한눈에 보기에도 비저빌리티 렌더링은 디퍼드에 비해 매우 매력적으로 보입니다. 10픽셀 크기의 트라이앵글의 경우 디퍼드 머티리얼 패스는 비저빌리티 머티리얼 패스보다 2배 더 많이 실행되어야 하며, 트라이앵글이 1픽셀인 경우 4배로 증가합니다. 하지만 비저빌리티 패스는 추가 작업이 필요합니다.
보간 및 부분 미분 분석
디퍼드 방식은 하드웨어에 의존하여 보간기를 픽셀 셰이더로 전달하지만, 우리는 이 데이터를 직접 가져와 보간해야 합니다. 첫 번째 단계는 데이터를 가져오는 것으로 비교적 간단합니다. 데이터를 적극적으로 패킹하면 상당한 이득을 얻을 수 있지만, 이 테스트에서는 단순화를 위해 데이터를 32비트 부동 소수점으로 저장합니다. g_dcElemData는 드로우 콜 요소 데이터로, 버텍스 버퍼가 시작되는 위치와 같은 중요한 인스턴스별 데이터를 포함하는 StructuredBuffer입니다.
uint3 FetchTriangleIndices(uint dcElemIndex, uint primId)
{
TriangleIndecis ret = (TriangleIndecis)0;
uint startIndex = g_dcElemData[dcElemIndex].m_visStart_index_pos_geo_materialId.x;
return g_visIndexBuffer.Load3(startIndex + 3 * 4 * primId);
}
TrianglePos FetchTrianglePos(uint dcElemIndex, TriangleIndecis triIndices)
{
uint startPos = g_dcElemData[dcElemIndex].m_visStart_index_pos_geo_materialId.y;
TrianglePos triPos = (TrianglePos)0;
triPos.m_pos0.xyz = asfloat(g_visPosBuffer.Load3(startPos + 12 * triIndices.m_idx0));
triPos.m_pos1.xyz = asfloat(g_visPosBuffer.Load3(startPos + 12 * triIndices.m_idx1));
triPos.m_pos2.xyz = asfloat(g_visPosBuffer.Load3(startPos + 12 * triIndices.m_idx2));
return triPos;
}많은 지침은 아니지만 성능을 저해하는 것은 데이터를 기다리는 시간입니다. UV와 일반 데이터를 가져오는 방법은 거의 동일하므로 여기서는 생략하겠습니다. 다음 단계는 바리센트릭 좌표를 계산하는 것입니다. DAIS 논문[12]에는 부록 A에 매우 편리한 공식이 있으며, ConfettiFX 코드도 매우 유용한 참고 자료입니다[4].
struct BarycentricDeriv
{
float3 m_lambda;
float3 m_ddx;
float3 m_ddy;
};
BarycentricDeriv CalcFullBary(float4 pt0, float4 pt1, float4 pt2, float2 pixelNdc, float2 winSize)
{
BarycentricDeriv ret = (BarycentricDeriv)0;
float3 invW = rcp(float3(pt0.w, pt1.w, pt2.w));
float2 ndc0 = pt0.xy * invW.x;
float2 ndc1 = pt1.xy * invW.y;
float2 ndc2 = pt2.xy * invW.z;
float invDet = rcp(determinant(float2x2(ndc2 - ndc1, ndc0 - ndc1)));
ret.m_ddx = float3(ndc1.y - ndc2.y, ndc2.y - ndc0.y, ndc0.y - ndc1.y) * invDet * invW;
ret.m_ddy = float3(ndc2.x - ndc1.x, ndc0.x - ndc2.x, ndc1.x - ndc0.x) * invDet * invW;
float ddxSum = dot(ret.m_ddx, float3(1,1,1));
float ddySum = dot(ret.m_ddy, float3(1,1,1));
float2 deltaVec = pixelNdc - ndc0;
float interpInvW = invW.x + deltaVec.x*ddxSum + deltaVec.y*ddySum;
float interpW = rcp(interpInvW);
ret.m_lambda.x = interpW * (invW[0] + deltaVec.x*ret.m_ddx.x + deltaVec.y*ret.m_ddy.x);
ret.m_lambda.y = interpW * (0.0f + deltaVec.x*ret.m_ddx.y + deltaVec.y*ret.m_ddy.y);
ret.m_lambda.z = interpW * (0.0f + deltaVec.x*ret.m_ddx.z + deltaVec.y*ret.m_ddy.z);
ret.m_ddx *= (2.0f/winSize.x);
ret.m_ddy *= (2.0f/winSize.y);
ddxSum *= (2.0f/winSize.x);
ddySum *= (2.0f/winSize.y);
ret.m_ddy *= -1.0f;
ddySum *= -1.0f;
float interpW_ddx = 1.0f / (interpInvW + ddxSum);
float interpW_ddy = 1.0f / (interpInvW + ddySum);
ret.m_ddx = interpW_ddx*(ret.m_lambda*interpInvW + ret.m_ddx) - ret.m_lambda;
ret.m_ddy = interpW_ddy*(ret.m_lambda*interpInvW + ret.m_ddy) - ret.m_lambda;
return ret;
}Edit (5/7/2022): 제임스 맥라렌(데시마 엔진 프로그래머) 과 스티븐 힐은CalcFullBary의 원래 버전에 잘못된 그라데이션이 있다는 사실을 발견했습니다. 제임스 맥라렌과 스티븐 힐의 업데이트된CalcFullBary 및 InterpolateWithDeriv 버전은 더 정확하고 GPU 래스터화 동작과 더 밀접하게 일치합니다.
입력 포인트는 동질 클립 공간( homogeneous clip space )에 있습니다(MVP 변환 직후). 원근 보간을 통해 바리센트릭 좌표(m_lambda)가 결정되므로 바리센트릭 좌표의 도함수(미분)를 x와 y를 기준으로 계산합니다. 마지막으로, 바이센트릭의 도함수는 2/winSize만큼 스케일링하여 스케일을 NDC 단위(-1에서 1)에서 픽셀 단위로 변경합니다. 마지막으로, NDC는 아래에서 위로, 창 좌표는 위에서 아래로 이동하기 때문에 m_ddy가 반전됩니다.
바이센트릭과 바이센트릭의 부분 도함수를 구하면 정점에서 어떤 속성이든 쉽게 보간할 수 있습니다. 세 개의 부동 소수점이 주어지면 이 함수는 보간된 값, 미분 x, 미분 y의 삼항식을 반환합니다.
float3 InterpolateWithDeriv(BarycentricDeriv deriv, float v0, float v1, float v2)
{
float3 mergedV = float3(v0, v1, v2);
float3 ret;
ret.x = dot(mergedV, deriv.m_lambda);
ret.y = dot(mergedV, deriv.m_ddx);
ret.z = dot(mergedV, deriv.m_ddy);
return ret;
}마지막으로 인터폴레이터에서 머티리얼 그래프의 텍스처 샘플까지의 경로에 있는 모든 값에 대해 체인 규칙을 적용합니다. 텍스처는 SampleGrad()를 사용하여 샘플을 샘플링하고 명시적으로 UV 도함수를 전달합니다.
또한 이것은 새로운 개념이 아니라는 점에 유의하세요. C++ 템플릿을 사용하여 이러한 방식으로 도함수를 생성하는 구현이 있으며[11], Arnold가 사용하는 접근 방식입니다[8]. 하지만 이 토이 엔진은 템플릿을 사용하여 파생 코드를 생성하는 대신 머티리얼 그래프에서 파생 계산을 hlsl로 생성합니다. 아놀드(소니 이미지 픽처스 아놀드 렌더러)는 실제로 파생물이 필요한 노드에 대해 '파생물 싱크'라는 용어를 사용하며, 싱크 경로에 있는 모든 노드는 이 경로를 따라 파생물을 계산해야 합니다. 그러나 이 경로에 있는 노드는 5~10%에 불과한 것으로 추정됩니다. 나머지 노드는 파생상품을 무시할 수 있습니다.
실제로 현실 세계의 대부분의 셰이더는 스케일과 회전과 같은 사소한 조정만으로 보간된 UV를 사용합니다. 머티리얼의 복잡성은 대부분 복잡한 수학과 UV 룩업 후 텍스처를 블렌딩하는 과정에서 발생합니다. 따라서 대부분의 경우 몇 개의 노드에서만 추가 파생 계산을 수행하면 됩니다.
그래도 상당한 추가 작업량입니다. 트라이앵글 밀도가 높아질수록 GBuffer 머티리얼이 2배 또는 4배 더 많은 호출을 필요로 함에도 불구하고 이러한 추가 명령어가 너무 무거워서 Visibility Material 함수가 GBuffer 머티리얼 함수보다 느린 것일까요? 아니면 이러한 추가 계산이 충분히 가벼워서 비저빌리티 머티리얼 함수가 더 빠를까요? 알아봅시다.
성능 테스트
테스트를 위해 하이트맵이 있는 단일 모델을 5x3 그리드에 복제했습니다. 카메라 아래에 그림자를 드리우는 메시도 여러 개 있습니다. 그림자 깊이 패스는 매우 많은 수의 트라이앵글의 깊이를 무차별적으로 렌더링하기 때문에 매우 비효율적이지만 세 가지 렌더링 유형 모두 비용이 동일하므로 숫자는 여전히 유효합니다. 또한 모든 명령(복사본 포함)은 그래픽 대기열에서 실행되어 중복을 최소화하고 일관된 수치를 얻습니다. 이 모든 샷의 타이밍 캡처는 1080p에서 NVIDIA RTX 3070(프레임 버퍼 크기가 16의 배수로 반올림되기 때문에 기술적으로는 1088)을 사용하는 내 컴퓨터의 PIX에서 캡처한 것입니다.

메인 그라운드는 하이트맵 메시의 5x3 그리드입니다. 테셀레이션된 하이트맵이 아닙니다. 그보다는 메시 포인트를 생성하는 전처리 단계가 있고, 그 다음에는 일반 메시처럼 처리됩니다. 아이디어는 삼각형의 대략적인 밀도를 제어하고 싶었지만 실제 사용 사례와 어느 정도 유사하게 보이도록 약간의 오버드로를 원했습니다. 해당 각도에서 그리기 호출은 다음과 같습니다:

이 설정을 사용하면 카메라를 고정하고 해당 메시의 해상도를 변경할 수 있으며 트라이앵글 수가 증가함에 따라 포워드, 디퍼드, 가시성 간의 트레이드 오프에 대한 대략적인 아이디어를 얻을 수 있습니다.
머티리얼 셰이더의 경우 게임에서 실제로 사용하는 것과 거의 비슷한 것을 원했습니다. 테스트 모델에서는 빠른 알베도, 노멀, 스페큘러 룩업을 수행하고 직접 출력하는 간단한 PBR 텍스처를 사용하는 것이 매우 일반적입니다. 하지만 현실 세계의 머티리얼 그래프는 스파게티 한 그릇처럼 보이는 경향이 있습니다. 이 셰이더는AmbientCg.com [ 2]의 텍스처 두 세트로 만들었는데, 허용된 라이선스에 따라 고품질의 무료 텍스처가 필요한 경우 적극 권장합니다.
PavingStones054
Ground037
블렌딩에는 3옥타브의 펄린 노이즈를 사용했습니다. 세 번째 레이어도 만들었는데 원래는 습윤성 레이어로 계획했습니다. 하지만 첫 번째 테스트에서 마른 가루처럼 보이는 플랫 레드가 마음에 들어서 이 레이어를 사용했습니다. 하이트맵과 결합된 펄린 노이즈의 옥타브가 혼합되어 빨간색 레이어가 돌 사이의 균열에 편향되어 있습니다.
다음은 머티리얼 그래프의 스크린샷입니다. 이 머티리얼 에디터에는 제대로 된 상용 엔진의 UI 기능이 대부분(전부?) 없기 때문에 약간 지저분합니다. 노드에 상수를 추가하는 방법을 몰라서 추가 노드가 많았습니다(예: 0.5를 추가하려면 추가 노드와 0.5 상수 노드가 모두 필요함). 하지만 이 테스트에는 충분했습니다.

Low Triangle Count
첫 번째 테스트에서는 큰 삼각형을 살펴볼 것이므로 각 메쉬는 두 개의 삼각형으로 이루어진 쿼드에 불과합니다. 아래는 로우 뷰이므로 얼마나 평평한지 확인할 수 있습니다.

다음은 삼각형 ID 보기입니다. 보시다시피 각 그리기 호출은 단지 두 개의 삼각형입니다.

최종 이미지.

몇 가지 숫자를 캡처해 보겠습니다. 다음은 패스에 대한 설명입니다.
PrePass: 포워드 및 디퍼드 패스의 경우 PrePass는 깊이만 기록합니다. 그러나 가시성 패스의 경우 drawCallId 및 triangleId를 포함한 가시성 U32도 씁니다.
Material: Deferred 패스의 경우 이 패스는 머티리얼 래스터화 패스를 참조합니다. Visibility의 경우 계산 패스의 시간을 나타냅니다. 물론 포워드 패스의 경우 이는 하나의 숫자를 위해 라이팅 패스와 병합됩니다.
Lighting: 지연된 경우 이 패스는 텍스처를 읽고 라이팅을 쓰는 컴퓨팅 셰이더입니다. Visibility는 텍스처 대신 버퍼를 사용하여 유사한 작업을 수행합니다.
VisUtil: 이 카테고리는 Visibility 렌더러의 다른 패스를 나타냅니다. 여기에는 각 머티리얼의 픽셀 수를 계산하고, 가시성 버퍼를 재정렬하고, 픽셀이 음영 처리되면 다시 선형 버퍼로 재정렬하는 계산 셰이더가 포함됩니다.
기타: 이 카테고리에는 다른 모든 패스가 포함됩니다. 여기서 주요 패스는 섀도 패스, TAA, 모션 벡터, 톤 매핑, GUI(이 스크린샷에는 나타나지 않음) 및 기타 배리어입니다. 실제로 계산한 방법은 총 GPU 시간에서 다른 모든 카테고리를 뺀 것입니다.
기타 카테고리는 렌더링 패스를 구성할 때 래스터/컴퓨트 중첩이 중요한 설계 결정 중 하나이므로 약간 까다롭습니다. 하지만 이 테스트의 목표는 최종 렌더링 시간을 최소화하는 것이 아니라 다양한 알고리즘 간의 상대적 비용을 결정하는 것입니다. 세 가지 렌더링 유형 모두 비용이 거의 비슷하므로 별도로 그룹화하는 것이 합리적입니다. 포워드/디퍼드/비저빌리티를 선택해도 TAA 및 섀도와 같은 항목의 비용에 미치는 영향은 미미합니다.
저밀도 트라이앵글 뷰 성능
PrePassMaterialLightingVisUtilOtherTotal
| PrePass | Material | Lighting | VisUtil | Other | Total | |
| Forward | 0.020 | 1.61 | 0.749 | 2.379 | ||
| Deferred | 0.020 | 1.06 | 0.730 | 0.759 | 2.569 | |
| Visibility | 0.043 | 1.06 | 0.762 | 0.322 | 0.832 | 3.01 |
그 결과는 흥미롭습니다. 지연된 경우 머티리얼 셰이더 비용은 1.06ms이고, 비저빌리티 셰이더 비용은 1.06ms로 어떻게 된 일인지 정확히 동일합니다. 또한 조명 셰이더 비용이 0.032ms로 약간 더 높고, 가시성 패스를 관리할 때 0.322ms의 오버헤드가 추가로 발생합니다. 마지막으로, 포워드 패스는 대역폭을 절약하기 때문에 머티리얼과 조명을 약간 더 빠르게 계산할 수 있습니다.
먼저, 5x3 쿼드는 거의 평평하고 약간의 z-파이팅이 있으므로 GBuffer 패스의 일부 픽셀이 올바른 초기 z 제거를 받지 못해 소량의 오버드로가 발생할 수 있습니다. 하지만 이 패스는 주로 대역폭이 제한되어 있기 때문에 버텍스 보간과 미분 계산에 드는 추가 ALU 비용이 대역폭 비용에 가려져 있다는 설명이 더 유력합니다.
하지만 수치를 보면 버텍스 어트리뷰트를 가져오고 부분 미분을 계산하는 추가 비용은... 아무것도 아니죠? 가시성 조명 패스가 약간 더 높고 추가 관리 패스가 합산되지만 전반적으로 다음 테스트를 위한 매우 고무적인 결과입니다. 또한 VisUtil 패스는 약간 낮아질 수 있습니다. 현재 구현은 텍스처 대신 버퍼를 사용하여 라이팅을 렌더링하고 나중에 데이터를 정렬합니다. 하지만 비저빌리티 데이터의 출력을 GBuffer에 UAV로 직접 저장하는 것이 더 빠를 것이 분명합니다.
중간 삼각형 수
다음으로 중간 해상도 보기를 시도해 보겠습니다. 고해상도 이미지의 경우 500x500으로 하겠습니다. 픽셀을 10배 더 가볍게 만들려면 500/sqrt(10)=158의 해상도로 만들 수 있습니다. 따라서 이 중간 해상도 설정의 메쉬는 158x158입니다. 디테일은 있지만 확실히 울퉁불퉁한 편입니다.

다음은 카메라 앵글에서 바라본 최종 화면입니다:

그리고 물론 모든 삼각형의 뷰입니다. 카메라 앵글을 잡을 때는 삼각형당 10픽셀 정도를 목표로 했는데, 언뜻 보기에는 8픽셀에 가까워 보입니다. 특정 크기가 아니라 트렌드를 포착하는 것이 목표이기 때문에 이 정도면 충분합니다.
삼각형이 약 8~10픽셀이라는 점을 감안하면 래스터화된 패스의 경우 약 2배의 비용이 들 것으로 예상할 수 있습니다. 그렇다면 수치는 어떻게 될까요?
PrePassMaterialLightingVisUtilOtherTotal
| PrePass | Material | Lighting | VisUtil | Other | Total | |
| Forward | 0.132 | 3.92 | 1.099 | 5.151 | ||
| Deferred | 0.132 | 2.95 | 0.764 | 1.122 | 4.968 | |
| Visibility | 0.158 | 1.65 | 0.818 | 0.336 | 1.188 | 4.15 |
참고로 기타의 변화는 섀도 뎁스 패스로 인해 발생하므로 그다지 중요하지 않습니다. 섀도 패스는 모든 지오메트리를 캐스케이드와 포인트 라이트 섀도 패스로 렌더링하는 매우 순진한 방식입니다. 지오메트리가 복잡해지기 때문에 섀도 패스도 복잡해집니다. 그러나 이러한 비용의 변화는 세 가지 렌더링 유형 모두에서 사실상 동일합니다. 세 가지 알고리즘의 관련 패스만 살펴보겠습니다: PrePass, Material , Lighting , VisUtil.
PrePass + Material + Lighting + VisUtil
| PrePass + Material + Lighting + VisUtil | |
| Forward (M) | 4.05 |
| Deferred (M) | 3.85 |
| Visibility (M) | 2.96 |
수치를 보면 삼각형이 작아질수록 가시성 렌더링이 앞선다는 것을 알 수 있습니다. 그리고 그 수치는 제가 생각했던 것만큼 가깝지 않습니다. 실제로 가장 먼저 눈에 띄는 것은 프리패스였습니다. (뎁스만 렌더링하는 것이 아니라) 가시성 ID와 뎁스를 모두 렌더링하면 성능에 더 큰 영향을 미칠 것으로 예상했지만, 비용 차이는 0.033ms로 매우 적었습니다. 가장 크게 증가한 것은 포워드 및 디퍼드 머티리얼 패스로, 이전 첫 번째 이미지에 비해 각각 2.43배와 2.78배의 길이가 늘어났습니다. 가시성 머티리얼 패스는 원래 패스 길이의 1.56배입니다.
그런데 왜 가시성 머티리얼 패스가 큰 삼각형의 경우보다 더 오래 걸릴까요? 결국 같은 수의 픽셀에서 실행되는 동일한 셰이더이기 때문입니다. 문제는 캐시 일관성입니다. 두 가지 시나리오를 살펴봅시다. 왼쪽에는 두 개의 삼각형으로 분할된 8x8 픽셀 블록이 있고, 오른쪽에는 8x8 블록의 각 픽셀이 다른 삼각형을 가리키고 있습니다.

컴퓨팅 셰이더에서 64개의 스레드 모두 첫 번째 버텍스에 대한 데이터를 가져옵니다. 하지만 왼쪽의 경우 GPU는 전체 8x8 블록에 대해 2개의 고유 버텍스 위치만 가져오면 됩니다. 그러나 오른쪽의 경우 GPU는 메모리 내 64개의 고유한 위치에서 가져와야 합니다. 일관성이 떨어질 뿐만 아니라 메모리에서 가져와야 하는 총 바이트 수가 더 많기 때문에 가져올 원시 대역폭도 더 많아집니다. 따라서 큰 삼각형을 사용한 첫 번째 테스트 사례에서는 이러한 추가 가져오기 비용이 사소한 수준이었지만, 이 장면에서는 관련 비용이 발생합니다. 하지만 이 비용은 지연 경로가 쿼드 사용률 저하로 인해 지불하는 페널티보다 훨씬 적습니다. 따라서 가시성 접근 방식이 전반적으로 더 빠릅니다.
높은 삼각형 수
마지막으로 삼각형 수가 많은 세 번째 스크린샷을 찍어 보겠습니다. 각 모델은 500x500이며, 삼각형당 1픽셀에 가깝습니다. 다음은 바위를 클로즈업한 사진입니다.

최종 이미지입니다:

그리고 삼각형 ID:

그렇다면 숫자는 어떻게 보일까요?
PrePassMaterialLightingVisUtilOtherTotal
| PrePass | Material | Lighting | VisUtil | Other | Total | |
| Forward | 1.00 | 9.27 | 4.726 | 14.996 | ||
| Deferred | 1.00 | 4.64 | 0.792 | 4.729 | 11.161 | |
| Visibility | 1.15 | 2.01 | 0.836 | 0.341 | 4.516 | 8.853 |
타임라인을 시작하면 프리패스 비용은 증가하지만 합리적인 수준을 유지하며, 비저빌리티 U32 작성 비용은 15%만 추가됩니다. 기타 패스도 크게 증가하지만 이는 주로 섀도 뎁스 패스에 의해 발생합니다. 가시성 패스는 기타 카테고리에서 0.21ms가 줄어드는데, 이는 약간 이상합니다. PIX 실행을 보면 섀도 뎁스 패스가 프리패스와 일부 겹치는 부분이 있으므로 프리패스의 추가 0.15ms 비용은 섀도 패스의 0.15ms를 숨기고 나머지 0.06ms는 VisUtil과의 다른 중복으로 숨겨져 있을 수 있습니다.
하지만 가장 큰 차이는 머티리얼 및 조명 비용입니다. 수치가 거의 모든 것을 말해줍니다. 포워드 비용은 첫 번째 프레임에 비해 5.76배, 디퍼드 머티리얼 비용은 첫 번째 프레임의 4.38배로 증가합니다. 하지만 가시성 머티리얼 비용은 첫 번째 프레임의 1.90배로 스케일링됩니다.
다시 한 번 렌더링 알고리즘 간의 차이와 관련된 패스를 분리해 보겠습니다.
PrePass + Material + Lighting + VisUtil.
| PrePass + Material + Lighting + VisUtil | |
| Forward (H) | 10.27 |
| Deferred (H) | 6.43 |
| Visibility (H) | 4.34 |
수치는 명확합니다. 이 테스트 사례에서 삼각형 밀도가 단일 픽셀로 줄어들면 가시성 렌더링의 쿼드 활용도가 향상되어 버텍스 속성을 보간하고 부분 도함수를 분석적으로 계산하는 데 드는 추가 비용이 훨씬 더 커집니다.
결론:원래 질문으로 돌아가서:
재료 그래프를 사용하여 분석 부분 도함수를 효율적으로 계산할 수 있습니까?
이 테스트 사례의 답은 "예"입니다. 하지만 일반적인 경우에는 "아마도"가 더 나은 대답입니다. 부분 파생물을 생성하는 데 필요한 추가 계산은 UV 스케일과 오프셋의 간단한 경우에는 사소한 것입니다. (전체 PIX 실행을 수행하지 않고) 몇 가지 다른 피상적인 테스트를 해본 결과, 수치를 근본적으로 변경할 만큼 성능 저하를 초래할 만큼 중요한 사용 사례는 없었습니다.
가장 일반적인 경우는 다른 텍스처의 UV가 되는 텍스처 출력입니다. 텍스처 읽기가 4개인 표준 머티리얼에 UV 오프셋 텍스처 읽기를 추가하는 경우 포워드/디퍼드 머티리얼 패스는 텍스처 읽기가 1개 추가되는 반면 가시성 머티리얼 패스는 3개가 추가됩니다. 하지만 텍스처 샘플 5개와 7개 사이의 차이는 수치를 크게 변경할 만큼 강력한 성능 절벽을 일으키지는 않습니다. 그리고 두 개의 추가 샘플은 첫 번째 샘플과 캐시 일관성이 매우 높기 때문에 비용이 최소화될 것으로 예상합니다.
더 문제가 되는 경우는 패럴랙스 오클루전 매핑입니다. 이론적으로는 각 단계마다 1개가 아닌 3개의 텍스처 읽기가 필요합니다. 하지만 실제로 각 단계에서 파생물이 그렇게 많이 바뀔까요? 모든 단계에 동일한 파생상품/밉맵 수준을 사용하는 것이 허용될까요? 언뜻 보기에는 합리적으로 보이지만 확인해보지 않았습니다.
그리고 물론 정말 나쁜 경우도 있습니다. 굴절 아이 셰이더는 각막 지오메트리 노멀에 따라 굴절할 때 뷰 벡터의 부분 도함수를 전달해야 합니다. 뷰 벡터의 x와 y의 미분과 각막 높이와 노멀의 x와 y의 부분 미분을 고려해야 하기 때문에 이 셰이더는 유한 차분 버전보다 3배 더 느리다고 상상할 수 있지만 비용을 줄일 수 있는 근사치도 생각해 볼 수 있습니다. 예를 들어 각막의 곡률이 너무 작아서 관련이 없다고 가정하고 계산에서 미분을 0으로 만들 수 있을 것 같습니다.
마지막으로 유한차를 사용하는 표준 미분도 완벽하지 않습니다. 분석 미분으로 전환하면 가지와 버림과 같은 문제를 우아하게 해결할 수 있는 경우가 있습니다. 특히 삼각형의 가장자리에서 벗어나는 헬퍼 레인을 사용할 때 더욱 그렇습니다.
따라서 이 경우에는 효과가 있습니다. 하지만 AAA 게임의 일반적인 부분 파생 문제와 관련하여 제 대답은 "아마도, 예에 기울어져 있다"입니다. 결론은 부분 파생 분석이 실행 가능할 가능성이 있지만, 더 복잡한 사용 사례에 대해서는 더 많은 테스트가 필요하다는 것입니다.
트라이앵글 수가 매우 많은 경우(트라이앵글당 1픽셀) 가시성 접근 방식이 더 빠를까요?
각 픽셀이 4번 실행되는 매우 많은 트라이앵글 수의 경우 가시성 렌더링이 확실한 승자입니다. 지연 비용은 6.43밀리초인 반면 가시성은 4.34밀리초입니다. 관련 패스에 대한 전체 GPU 비용이 32.5% 감소한 것은 사소한 일이 아닙니다.
일반적인 삼각형 크기(삼각형당 5~10픽셀)는 어떨까요? 이 경우에도 가시성 접근 방식이 더 빠를까요?
이 테스트에서 중간 개수의 경우, 네, 가시성 접근 방식이 더 빠릅니다. 하지만 그 차이는 3.85ms 대 2.96ms로 더 가깝습니다. 그래도 23.1%의 감소는 사소한 것이 아닙니다. 또한 지오메트리와 오버드로가 많은 나쁜 시야각에서는 가시성 접근 방식이 스파이크가 덜할 것으로 예상하지만 이는 추측일 뿐입니다.
기타 고려 사항:
트라이앵글 수가 많을 경우 가시성 렌더링이 디퍼드보다 더 잘 확장되고 트라이앵글 수가 매년 증가하고 있다는 점을 고려할 때 모든 게임 엔진이 모든 것을 중단하고 전환해야 할까요? 당연히 아니죠. 주요 아키텍처 렌더링 결정에는 몇 가지 다른 요소도 있습니다.
코드 복잡성:
가시성 렌더링에 대한 가장 큰 반대 논거는 아마도 복잡성일 것입니다. 가시성 렌더링은 버텍스 버퍼와 부분 파생물을 관리하는 데 엔지니어링 시간이 필요합니다. 엔지니어링 시간은 무한하지 않습니다.
메모리:
가시성 렌더링을 사용하려면 모든 동적 지오메트리가 셰이더에서 액세스할 수 있는 거대한 버퍼(또는 버퍼)에 있어야 합니다. 화면이 풀잎으로 덮여 있다면 변형 후 버텍스 하나하나가 모두 버퍼 어딘가에 있어야 합니다. 그렇긴 하지만 메모리가 생각만큼 나쁘지는 않습니다. XYZ 위치를 각각 16비트로 패킹할 수 있으므로 각 버텍스는 6바이트가 됩니다. 변형 후 탄젠트 공간이 필요한 경우 픽셀당 총 10바이트의 4바이트 쿼터니언에 저장할 수 있습니다. 1080p(200만 픽셀)로 렌더링하고 픽셀당 버텍스가 하나라고 가정해 보겠습니다. 그러면 20MB의 RAM이 필요하고, 이전 프레임도 저장해야 한다면 40MB가 필요합니다. 40MB의 RAM은 사소한 수준은 아니지만, 그렇다고 터무니없는 수준도 아닙니다. 그리고 레이트레이싱에 메시를 포함하려면 변형 후 버텍스가 필요합니다.
PSO 스위치:
가시성 렌더링의 미묘한 장점 중 하나는 래스터화 중 PSO 전환 횟수가 적다는 점입니다. 포워드 또는 디퍼드 래스터화 패스에서 픽셀 셰이더가 이전 단계의 작업으로 인해 고갈되면 특히 PSO가 계속 전환되는 경우 버블이 발생할 수 있습니다. 그러나 불투명 지오메트리는 완전히 다른 머티리얼을 사용하더라도 동일한 가시성 픽셀 셰이더를 공유할 수 있습니다. 몇 가지 예외(백페이스 컬링, 알파 테스트 등)가 있지만, 모든 보이는 지오메트리를 삼각형 ID 쓰기 패스에 대해 몇 개의 PSO로만 그룹화할 수 있습니다. 또한 머티리얼 패스에서 PSO를 보다 적극적으로 그룹화할 수도 있습니다. 예를 들어, 불투명 렌더링을 하는 머티리얼과 알파 테스트가 있는 베리에이션은 동일한 비저빌리티 간접 CS 디스패치에서 머티리얼 데이터를 평가할 수 있지만, 디퍼드 머티리얼 패스에서는 별도의 PSO가 필요합니다. 비저빌리티 파이프라인은 버블이 훨씬 적어야 하지만 이러한 종류의 워크로드를 테스트하는 것은 작은 토이 엔진의 범위를 벗어납니다.
머티리얼 비용:
거대하고 복잡한 머티리얼로 렌더링하는 경우 가시성이 더 중요합니다. 버텍스 데이터를 가져오고 보간하는 데 드는 비용이 머티리얼 평가 비용에 숨겨져 있기 때문입니다. 짧은 머티리얼 셰이더로 렌더링하는 경우 보간 비용과 고정 비용 오버헤드가 더 많이 노출됩니다.
최소 사양:
이 테스트는 가까운 시일 내에 출시될 AAA 게임의 최소 사양보다 높은 NVIDIA GTX 3070에서 수행되었습니다. 특히 이 테스트 사례의 고정 비용은 약 0.34ms입니다. 그러나 5년 전의 저가형 노트북 GPU에서 동일한 비용이 발생한다면 상당히 가파르게 상승할 것입니다. 가시성은 훨씬 더 강력해질 미래의 GPU에는 잘 확장되지만, 반대로 오랫동안 최소 사양에 머물러 있을 과거의 GPU에는 확장성이 떨어집니다.
해상도 업스케일링:
두 번째로 고려해야 할 사항은 NVIDIA의 DLSS[10], AMD의 슈퍼 해상도[1], 언리얼의 템포럴 슈퍼 해상도[6] 같은 업스케일링 알고리즘의 역할입니다. 물론 의견은 다를 수 있지만, 셰이딩이 잘린 4K 기본 해상도와 4K로 업스케일된 고품질 셰이딩이 적용된 1080p 이미지 중에서 선택할 수 있다면 저는 업스케일된 1080p를 택할 것입니다. 하지만 삼각형당 10픽셀의 4K 이미지를 타겟팅하고 있다가 1080p로 전환하기로 결정했다고 가정해 보겠습니다. 10픽셀 트라이앵글이 갑자기 2.5픽셀 트라이앵글로 바뀝니다. 다시 말해, PS4/XB1에서 트라이앵글 수를 늘리되 해상도를 1080p 프레임버퍼를 목표로 유지하면 PS5/XSX에는 매우 작은 트라이앵글이 많이 생기게 됩니다.
쿼드 활용도 중요성:
여기서 중요한 결론은 쿼드 활용도가 중요하다는 것입니다. 사실상 오버드로와 동일한 비용입니다! 우리는 모두 1픽셀 삼각형이 나쁘다는 것을 알고 있지만 10픽셀 삼각형도 이상적이지 않습니다. 4배는 2배보다 나쁘지만 2배도 1배보다 나쁩니다. 쿼드 사용률은 미래의 먼 문제가 아닙니다. 현재 게임이 실제로 출시되는 워크로드에서 쿼드 사용률은 실제 문제입니다. 하지만 쿼드 활용도를 해결하면 실제로 렌더러를 최적화하고 헬퍼 레인 대신 흥미로운 효과를 위해 GPU 사이클을 사용할 수 있는 여지가 많습니다.
https://ko.wikipedia.org/wiki/%EB%AF%B8%EB%B6%84#:~:text=%EB%AF%B8%EB%B6%84(%ED%95%9C%EA%B5%AD%20%ED%95%9C%EC%9E%90%3A%20%E5%BE%AE%E5%88%86%2C,%EA%B5%AC%EC%84%B1%EB%90%98%EB%8A%94%20%EC%83%88%EB%A1%9C%EC%9A%B4%20%ED%95%A8%EC%88%98%EB%8B%A4.
REFERENCES:
[1] AMD FidelityFX, Super Resolution. AMD Inc. (https://www.amd.com/en/technologies/radeon-software-fidelityfx-super-resolution)
[2] AbientCG, (https://www.ambientcg.com)
[3] The Visibility Buffer: A Cache-Friendly Approach to Deferred Shading. Christopher Burns and Warren Hunt. (http://jcgt.org/published/0002/02/04/)
[4] ConfettiFX/The-Forge. ConfettiFX. (https://github.com/ConfettiFX/The-Forge)
[5] 4K Rendering Breakthrough: The Filtered and Culled Visibility Buffer. Wolfgang Engel. (https://www.gdcvault.com/play/1023792/4K-Rendering-Breakthrough-The-Filtered)
[6] Unreal Engine 5 Early Access Release Notes. Epic Games, Inc. (https://docs.unrealengine.com/5.0/en-US/ReleaseNotes/)
[7] Nanite, Inside Unreal. Brian Karis, Chance Ivey, Galen Davis, and Victor Brodin. (https://www.youtube.com/watch?v=TMorJX3Nj6U)
[8] Sony Pictures Imageworks Arnold. Christopher Kulla, Alejandro Conty, Clifford Stein, and Larry Gritz. (https://dl.acm.org/doi/10.1145/3180495)
[9] HLSL Shader Model 6.0, Microsoft Inc. (https://docs.microsoft.com/en-us/windows/win32/direct3dhlsl/hlsl-shader-model-6-0-features-for-direct3d-12)
[10] NVIDIA DLSS. NVIDIA Inc. (https://www.nvidia.com/en-us/geforce/technologies/dlss/)
[11] Automatic Differentiation, C++ Template and Photogrammetry. Dan Piponi. (http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.89.7749&rep=rep1&type=pdf)
[12] Deferred Attribute Interpolation for Memory-Efficient Deferred Shading. Cristoph Schied and Carsten Dachsbacher. (http://cg.ivd.kit.edu/publications/2015/dais/DAIS.pdf)
함께 볼만한 내용.
SIGGRAPH 2021 REAC: Geometry Rendering Pipeline Architecture at Activision
원문
Visibility Buffer Rendering with Material Graphs – Filmic Worlds
Visibility Buffer Rendering with Material Graphs
filmicworlds.com
